elektrochem. Membranpotential
Nernst-Potential
In einem System befinden sich 2 Phasen, getrennt durch eine semipermeable Membran (für \( K^+ \) permeabel) und nur 1 Paar Ionen ( \(A^- \) und \( K^+ \)). Entsprechend der Boltzmann-Verteilung diffundiert \( K^+ \) entlang des elektrochem. Gradienten. Es wirken also 2 entgegengesetzte Kräfte auf das \( K^+\)-Ion: die treibende Kraft des Konzentrationsausglieches und eine elektrostatische Kraft, die durch die Diffusion und die ungleichmäßige Verteilung von Landungen entsteht. Im Gleichgewicht gilt \( \tilde\mu_{K_1} = \tilde\mu_{K_2}\), was zu einem elektrischen Gradienten führt. Beim einsetzen in die Form einer Pfaffschen Differentialgleichung erhält man die:
Nernst-Gleichung
\[ \Delta\Psi = \phi_2 -\phi_1 = \frac{RT}{z_{K}F} \ln{\frac{c_{K_1}}{c_{K_2}}} \] Bei gleichen Standardpotentialen gilt: \[ U=60\,mV*\log{\frac{c_{ausen}}{c_{innen}}} \] beschreibt das Membranpotential, welches sich bei ungleicher Verteilung von membranpermeabeln Ionen einstellt.
Strom/Spannungskurven
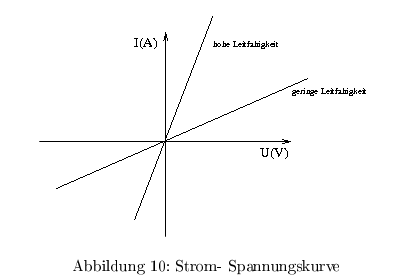
unter der Bedingung \( K^+_{ausen}:K^+_{innen}=0,1 \) ergibt sich folgender Verlauf:
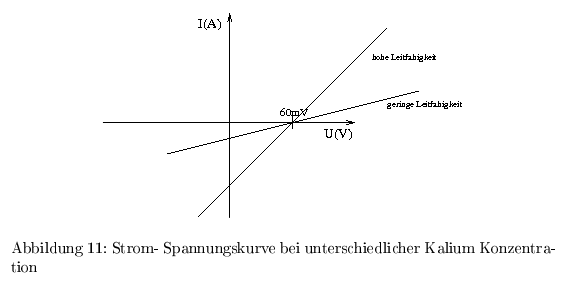
Donnan-Potential
Die Beeinflussung durch nicht-permeable Ionen/Proteine. im Gleichgewicht gilt: das chemische Potential \( \mu \) der einzelnen Ionen ist auf beiden Seiten der Membran gleich. Das Verhältnis der Konzentrationen ist durch die Donnan ratio ( \(r\) ) beschrieben:
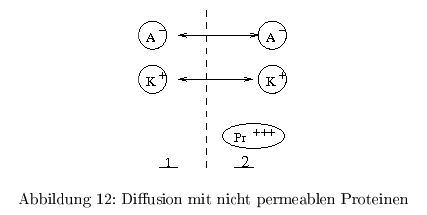
\[ \begin{align} \frac{c_{A^-_{2}}}{c_{A^-_{1}}} &= \frac{c_{K^+_{1}}}{c_{K^+_{2}}} = r \\ &= \exp{\frac{F\Delta\Psi}{RT}} \end{align} \] Man beachte, dass das Verhältnis der Anionen umgekehrt proportional dem Verhältnis der Kationen ist. es ergibt sich so die Gleichung für das Donnanpotential \( \Delta\Psi \) \[ \Delta \Psi = \frac{R \ T}{F} \ln(r) \] mit Hilfe der Elektroneutralitätergibt sich: \[ \begin{align} 0= r^2 - \frac{z*c_{Pr^+}}{c_{K_1^+}}*r-1 \end{align} \] durch Lösen der quadratischen Gleichung erhält man: \[ \begin{align} r= \frac{1}{2}\frac{z*c_{Pr^+}}{c_{K_1^+}} \pm \sqrt{\left(\frac{1}{2}\frac{z*c_{Pr^+}}{c_{K_1^+}}\right)^2+1} \end{align} \] Die Lösung: Donnan-Graph
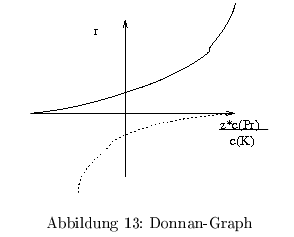
Lebende Systeme sind jedoch nicht im Gleichgewicht und die Ionenpumpen lassen sich nur näherungsweise beschreiben. Des weiteren wurden mögliche Volumenänderungen außer Acht gelassen und damit die Verdünnung der Ladungsträger.
thermodyn. Betrachtung von Fluxen
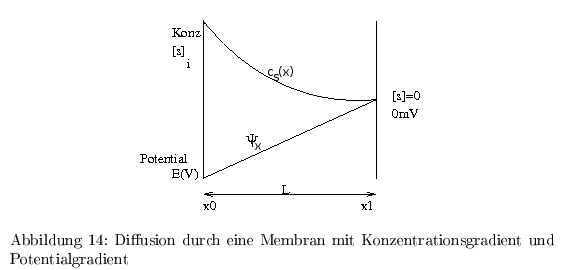
Die Diffusion von ungeladenen Teilchen entlang eines Konzentrationsgradienten folgt dem 1. Fickschen Gesetz: \[ \Phi_s = -D_s \frac{dc_s}{dx} [\frac{mol}{cm^2\,s}] \] ( \( \Phi_s = \) molare Partikelflussdichte) und ( \( D= \) Diffusionskoeffizient) Das lösen der Differentialgleichung führt zu: \[ \begin{align} - \frac{dc}{dx}=\frac{\Phi_s}{D_s}=\frac{c_s *v}{D_s}= A*\exp\left(-\frac{v}{D_s}x\right) \end{align} \] Die Konzentration fällt also exponentiell, während für geladene Teilchen in einem elektrischen Feld folgender linearer Ansatz gilt: \[ \begin{align} \Phi_s &= -U_s *c_s \frac{d\varphi}{dx} \\ J_s &= -z_s\,F\ \frac{d\varphi}{dx}\ M_s\,c_S \\ &= \underbrace{\frac{-z_s\,F\,U_s\,c_s}{L}}_{Leitfahigkeit\ (g)} * E\\ &= g*E\\ \end{align} \] ( \( U_s = \) Verschiebungsgeschwindigkeit: net drift velocity) und ( \(\varphi = \) elektr. Potential) und ( \( J_s = \) der Elektrolytflux von \( s \) )
Nernst-Planck-Gleichung
Die Nernst-Planck-Gleichung beschreibt die Flussdichte ( \( \Phi_i \) ) von Ionen im elektrischen und Konzentrationsgradienten und stellt eine Art Kombination aus Ohmschen Gesetz und Kohlrauschen Verschiebungsgestz dar. Die Flussdichte setzt sich also als Summe aus Diffusionsanteil und elektrischem Feld zusammen: \[ \Phi_i = (\Phi_i)_{Diff}+(\Phi_i)_{el} \] Wobei nach 1. Fick'schen Gesetz der Diffusionsanteil durch den Diffusionskoeffizienten ( \( D_i\) ) und durch den Konzentrationsgradienten ( \( \frac{dc_i}{dx} \) ) gegeben ist. Der Anteil des elektr. Feldes ergibt sich nach Kap. "thermodyn. Fluxe" und so erhält man die Nernst-Planck-Gleichung für den Gesamtfluss: \[ \Phi_i = -D_i \left(\frac{dc_i}{dx}+z_i\,c_i\ \frac{F}{RT}\,\frac{d\varphi}{dx}\right) \]
Goldmann-Hodgkin-Katz-Strom-Gleichung
\[ J_s = P_s\,A \ \frac{[s]_{innen}-[s]_{ausen}*\exp\left(-\frac{z\,F\,E}{R\,T}\right)}{1-\exp\left(-\frac{z\,F\,E}{R\,T}\right)} \] mit \( A=z^2\,\frac{E\,F^2}{R\,T} \) erlaubt die Berechnung absoluter Permeabilität aus Strommessungen bei verschiedenen bekannten Spannungen für den Fall, dass sich ein Ion in beide Richtungen bewegt. Man unterscheidet also folgende 2 Fälle:
- Strom aus der Zelle heraus: \[ J_s\rightarrow out = P_sA \frac{[s]_{innen}}{1-\exp\left(-\underbrace{\frac{z\,F\,E}{R\,T}}_{E\gg 0=0}\right)} \] Bei sehr hohen positiven Strömen ( \( E\gg 0 \) ) wird der ausströmende Ionenflux linear. \newline \( J_s \rightarrow out = P_s*A*[s]_{innen} \)
- Strom in die Zelle herein: \[ \begin{align} J_s\leftarrow in &= -P_sA\,\frac{[s]_{ausen}\,\exp\left(-\frac{zFE}{RT}\right)}{1-\exp\left(- \frac{zFE}{RT}\right)} \\ &= P_sA\,\frac{[s]_{ausen}}{1-\exp\left(\underbrace{\frac{zFE}{RT}}_{E\ll 0 = 0}\right)} \end{align} \] Bei sehr hohen negativen Strömen ( \( E\ll 0 \) ) wird der einströmende Ionenflux linear.\( J_s \leftarrow in = P_s*A*[s]_{ausen} \)
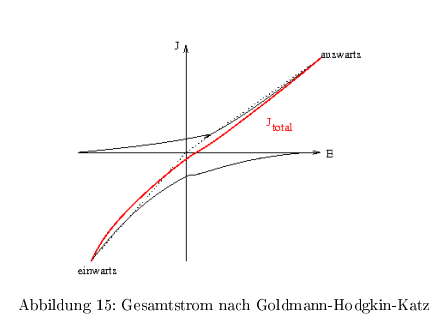
Der Gesamtstrom \( J_{total} \) aus Addition der Ein- und Auswärtsstroms bei unterschdl. Ionenkonzentration ist nicht linear und geht nicht durch Null!
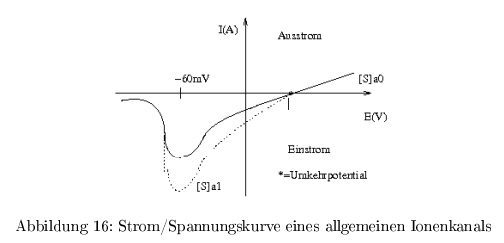
Strom-Spannungskurven eines Ionenkanals
GHK-Spannungsgleichung
Die Goldmann-Hodgin-Katz Voltage Equation beschreibt das Diffusionspotential unter Berücksichtigung von passiven Ionenströmen, ohne auf Ladungsfluss durch Ionenpumpen etc. einzugehen. \[ \Delta\psi = \frac{RT}{F}\ \ln\frac{\sum [c^-]_{innen} + \sum [c^+]_{ausen}}{\sum [c^-]_{ausen} + \sum [c^+]_{innen}} \] Bei Betrachtung von nur einem Ion erhält man die Nernst-Gleichung
Barrieren in geladenen Membranen
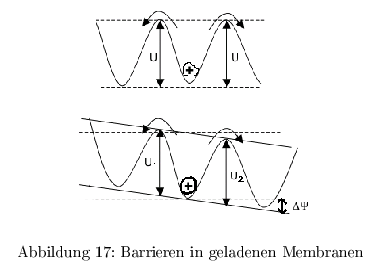
Die Geschwindigkeit der Ionen ist bestimmt durch eine lineare Funktion ( \( \Delta\Psi(E) \) ) und eine exponentielle Funktion der Energiebarrieren: \[ V_s =V_{rein}-V_{raus} \approx \frac{zFs\Delta\Psi}{RT} \exp\left(-\frac{U}{RT}\right) \]
Ionenpermeation und Dehydratisierung
Ionen liegen in Wasser solvatisiert vor. Die Wärme, die frei wird, wenn Ionen in Wasser gelöst werden ist die Hydratationsenthalpie \( \Delta H \)
- Selektive Ionenkanäle beruhen auf dem "Abstreifen" der Hydrathülle (=stripping)
- Wasser wird durch polare Seitengruppen des Ionenkanals ersetzt
- erfolgt mehrmals bei der Translokation
Hydratationsenergie um ein Ion durch einen Ionenkanal zu transportieren in der Näherung von M. Born \[ \begin{align*} \Delta G &= \frac{z^2q_e^2N}{r\,8\pi\,\epsilon_0}\left(\frac{1}{\epsilon_2}-\frac{1}{\epsilon_1}\right) \\ &= \frac{z^2}{r} * 166 * \left(\frac{1}{\epsilon_2}-\frac{1}{\epsilon_1}\right) \end{align*} \] ( \( \epsilon = \) Dielektrizitäts-Konstanstante) Die Bewegung von \( H^+ \) ist in Poren sehr schnell, obwohl \( \Delta H \) groß ist \( \rightarrow \) Erklärung: Relay-Mechanismus Protonenhüpfen = Umorientierung des H-Brücken-Netzwerkes Man unterscheidet:
- Strömungspotential: Wasser bewegt sich durch die Pore und nimmt Ionen mit
- Elektroosmose: bei hohem Ionenfluss bewegt sich Wasser mit