1. Home
2. Downloads
3. Study Material
4. Photobiophysik

Biologische Makromolekühle (DNA, RNA, Proteine) absorbieren Licht mit \( \lambda < 300\,nm \) und Proteine mit Co-Faktoren wie Chlorophyll, Flavine, Retinal etc. absorbieren zusätzlich im sichtbaren Bereich ( \( \lambda = 300-900\,nm \) ). Absorptionsänderungen geben Informationen über struckturelle Änderungen, \(e^-\)-Transportprozesse, Redoxreaktionen mit extrem hoher Zeitauflösung

Quantifizierung der Lichtabsorption

Im Bereich des sichtbaren Lichtes liegen 2 Wechselwirkungen mit Materie vor: Streuung und Absorption. Lichtabsorption ist nach der Quantentheorie möglich, wenn die Energie eines Quants der Energiedifferenz zweier atomarer oder molekularer Zustände entspricht. Das ist der Grund für das Auftreten von diskreten Linien im Absorptionsspektrum. Der Schwächungskoeffizient \( \mu = \sigma N_z \) gibt die Wahrscheinlichkeit der Absorption eines Quantes an. ( \( \sigma= \) Wechselwirkungsquerschnitt) und ( \( N_z= \) Teilchenkonzentration)

Lambert-Beersches Gesetz

\[ \begin{align} I &= I_0 \exp(-\sigma n s) \\ \sigma *n &= \ln{10} \frac{n}{N_L} \epsilon \\ \log\frac{I}{I_0} &= -\epsilon c s \end{align} \] ( \(n = \) Zahl der Molekühle) und ( \(s = \) die zurückgelegte Strecke) und ( \(\epsilon = \) der molekularer Extinktionskoeffizient) \[ E=\epsilon*c*s=\log\frac{I_0}{I} \] Die gemessene Extiktion ( \( E \) ) enthält streng genommen auch Lichtstreuung. Absorptionsspektren: \( E=E(\lambda) \)

• relative Spektren: Auftragen von \( E \) gegen \( \lambda \)
• absolute Spektren: Anzahl der Photonen die pro Molekühl und Wellenlänge absorbiert werden. Auftragen von \( \sigma \) gegen \( \lambda \)

Absorptions- und Emissionsprozesse

Bei der Absorption eines Lichtquantes wird ein Elektron auf eine Bahn höherer Quantenzahl angehoben. Man unterscheidet 2 qualitativ unterschiedliche Grundzustandsklassen: \( S_0, S_1, S_2 \dots \) und \( T_1, T_2, T_3 \dots \) . In den Singulettzuständen \( S \) weisen die Elektronen antiparallelen Spin auf. In den Triplettzuständen \( T \) jedoch parallel zueinander ausgerichteten Spin. Nach dem Pauli-Prinzip müssen sich die Elektronen jedoch in einer anderen Quantenzahl unterscheiden. Die beiden Zustände unterscheiden sich deutlich in ihre Lebenszeit. Die Triplettzustände weisen dabei eine höhere Stabilität auf als die \( S \)-Zustände. Die einzelnen Grundzustände besitzen eine Vielzahl von Schwingungs- und Rotationszustände. Ist die Energie eines Quants höher als die Energiedifferenz der einzelnen Grundzustände, wird das Elektron in ein höher liegendes Schwingungs- oder Rotationsniveau gehoben und anschließend über therm. Schwingungsrelaxation ins Grundniveau überführt.

Jablonski Diagramm

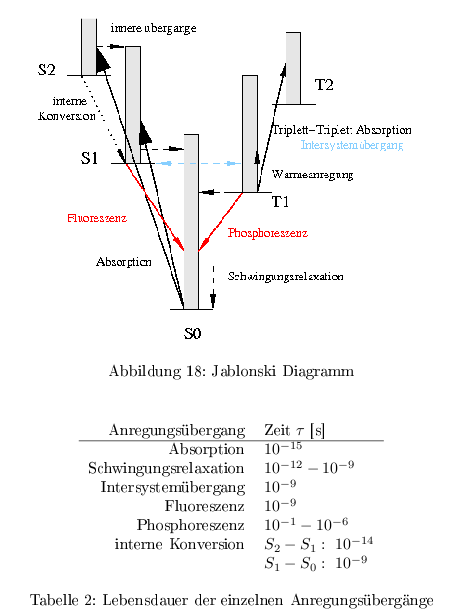
Angeregte Singulettzustände werden durch Absorption direkt erreicht, wohin Triplettzustände nur durch Intersystemübergänge erreicht werden können. Ein Übergang \( T_1\rightarrow S_1 \) ist energetisch nicht möglich, da die Triplettzustände weniger Energie enthalten. Bei Strahlungslosen Übergängen wird die überschüssige Energie in Form von Wärme frei.

Flourenszenzlebensdauer

Wenn mit Hilfe eines Lichtblitzes Atome in einen angeregten Zustand überführt werden, dann gilt folgende zeitabhängigkeit: \( N_1(t)=N_1^0 e^{-kt} \) mit \( k=k_s + k_F \). ( \(k_s = \) strahlungslose Übergänge) und ( \(k_F = \) Inaktivierung durch Fluoreszenz) Die mittlere Lebenszeit des angeregten Zustandes ist durch \( \tau = 1/k_s+k_F \) gegeben und damit ist die Fluoreszenzlebensdauer von allen Inaktivierungsprozessen abhängig. \[ \begin{align} \Phi_{Fl} &= \frac{\tau_{Fl}}{\tau_{rad}} \\ k_{Fl}&=\frac{1}{\tau_{rad}} \end{align} \] ( \(FL= \) Fluoreszenzquantenausbeute) und ( \(\tau_{Fl} = S_1 \) Lebenszeit) und( \(\tau_{rad}= \) radiative lifetime, Inaktivierungszeit über reine Fluoreszenz) und ( \(k_{Fl}= \) Fluoreszenzkonstante)

Born-Oppenheimer Näherung

Die Beziehungen zwischen Elektronen und Kern sind definiert durch die Energie (Coulomb und kinetisch) und quantenmechanisch als Wellenfunktion. In der Näherung wird ein Molekühl als harmonischer Oszillator mit konstantem Abstand zwischen den Kernen angenommen. Die Bewegung der Elektronen wird wegen des großen Masseunterschiedes von Elektronen und Kern als vom Kern unabhängig betrachtet. \[ \Psi_{n,\upsilon}= \Psi_n(r,R) * K_{n,\upsilon}(R) \] Die Totale Wellenfunktion mit \( n= \) elektr. Zuständen und \( \upsilon= \) Schwingungszuständen. \( r \) beschreibt die \( e^--e^- \) Wechselwirkungen, \( R \) die \( e^--\) Kern WW, und \( K \) die Kern-Kern WW.

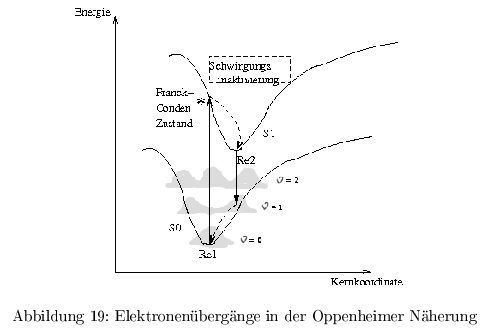
\( Re1 \) ist der Gleichgewichtszustand für \( \epsilon =0 \). Die Potentialkurve beschreibt Molekühle als harmonischen Oszillator, die Schwingungsniveaus können aber nur diskrete Werte \( \epsilon_{0 \dots n} \) annehmen, da die Energie in bewegungseingeschränkten Systemen gequantelt ist. Die Potentialkurven sind außerdem unsymmetrisch, da Molekühle bei zu starker Anregung zerfallen. Bei der Absorption findet ein elektr. Übergang ( \( \tau <10^{-15}s \) ) ohne Änderung der Kernkoordinate statt. \( K_{n,\upsilon}=const. \) Danach folgt eine Schwingungsrelaxation ( \( \tau \approx 10^{-15}-10^{-12} \) ), wobei die Energie in Form von Wärme abgegeben wird. (vibrational cooling) Die Fluoreszenz ( \( \tau \approx 1\,ns \) ) geht immer vom GG-Zustand \( Re \) ( \( \epsilon =0 \) ) aus (Regel von Kaska), da die Schwingungsrelaxation viel schneller ist.

• Absorption: erfolgt von einem Schwingungsgrundzustand in einen elektr. angeregten Schwingungszustand.
• Emission erfolgt vom elektr. angeregten Schwingungsgrundzustand in einen angeregten Schwingungszustand

Die daraus resultierende Energiedifferenz bezeichnet man als stroke shift und äußert sich in der Farbverschiebung von Absorption und Emission. Die Differenz ist groß, wenn sich die Kernabstände von \( S_0 \) und \( S_1 \) stark unterscheiden. Das Übergangsmoment für einen elektr. Übergang ist ein Vektor aus dem "Produkt" von 2 Wellenfunktionen. Mit der Born-Oppenheimer Näherung und der Vernachlässigung der Änderung der Kern-Kern-WW vereinfacht sich das Übergangsmoment zu: \[ \mu_{1,2} = \mu_{el;1,2}*S_{1,2} \] ( \(S = \) Frank-Condon Faktor)

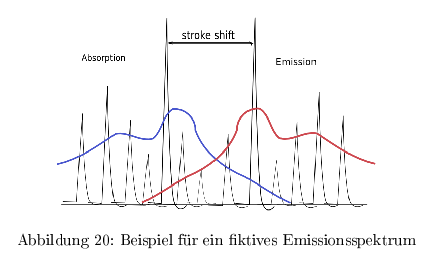
Emissionsspektren

Auf der Energieskala sind Excitations- und Emissionsspektren spiegelsymmetrisch auf der \( \lambda \)-Skala ist das Excitationsspektrum jedoch schmaler. Da Molekühle keine homogene starre Systeme sind, kommt es durch die Vielzahl an Schwingungsstadien zu einem mehr oder weniger ausgefranzten Spektrum.

Zeitauflösung

\[ S(t) = S_{max} *\sigma *\exp\left(-\frac{t-t_0}{\tau_{Fl}}\right) \]

Fluoreszenzpolarisation

Die Voraussetzung ist die Anregung mit polarisiertem Licht. Der Grad der Fluoreszenzpolarisation wird durch Vergleich des Fluoreszenzsignals parallel zur Anregung und senkrecht zur Anregung ermittelt. \[ P_F = \frac{S_{F_\parallel}-S_{F_\perp}}{S_{F_\parallel}+S_{F_\perp}} \] Die Abklingzeit der FP gibt Informationen über die Rotation und Größe der Molekühle.

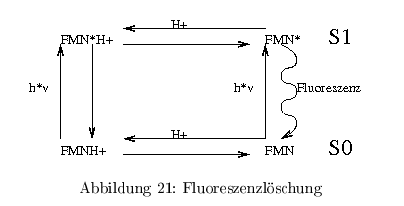
Fluoreszenzlöschung (quenching)

Die Fluoreszenz eines biolog. Chromophors kann durch Wechselwirkungen und Reaktion mit anderen Molekühlen (H\(^+\), Trp, Phe, \( e^-\)-Überträger) beeinflusst werden.

1. Fuoreszenzlöschung im Dunkeln (statisches quenching)
2. Löschung im Licht (dynamisches quenching)

Green-Fluorescent-Protein (GFP)

Protein aus der Qualle Aequorea victorea und das am weitesten verbreitete Markerprotein in der Zellbiologie für Proteinlokalisation, Quantifizierung, Expression, Protein-WW etc. Fluoresziert bei mechanischer Bewegung: \( Ca^{2+} \) Einstrom \( \rightarrow \) blaue Luminizenz des \( Ca^{2+}\)-Bindeproteins Aequorin \( \rightarrow \) Energieübertragung auf GFP \( \rightarrow \) grüne Fluoreszenz GFP ist extrem stabil und benötigt keinen externen Chromophor. GFP ist nur in der deprotonierten Form (GFP II) stark fluoreszierend bei \( 503\,nm\). Die protonierte Form (GFP I) fluoresziert nur schwach bei \( 510\,nm\)

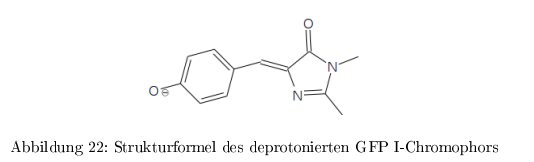
Die folgende Grafik veranschaulicht die einzelnen Formen des GFP-Chromophors und ihre Fluoreszenz:

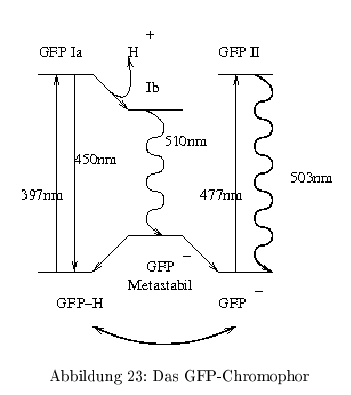
Dieser Prozess läuft bei einem \( pH>10 \) ab, was den Bedingungen innerhalb des Proteins entspricht. Die Synthese des GFP-Chromophors ist an die Anwesenheit von \( O_2 \) gebunden und damit in anaeroben Systemen unbrauchbar.

Bakteriorhodopsin

Die natürliche Funktion ist die Konvertierung von Licht in einen elektrochem. Gradienten und ist eine Art "primitive" Photosynthese von Archaea und marinen Eubakterien (vektorieller Transport) Der biologische Photorezeptor besteht dabei aus einem korrekt gefaltetem Protein und einem lichtempfindlichen organischen Chromophor. Der Chromophor in mikrobiellen Rhodopsinen ist Retinal gekoppelt mit Lysin des Proteins über eine Schiff'sche Base.

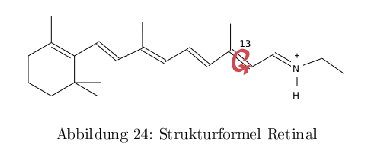
Die Proteinumgebung bestimmt dabei die Ladungsverteilung des Polyensystems und damit die Wellenlänge der Absorption. Nach einer Belichtung erfolgt eine Rotation um die \( C_{13}-C_{14} \) Bindung von all-trans-Retinal zu --> 13-cis-Isomerisierung.
Vorgang:

• Lichtabsorption: \( S_0 \rightarrow S_1 = 10^{-15}\,s \)
• Isomerisierung: \( 10^{-12}\,s \), Quantenausbeute: \( \phi = 0,3-0,6 \)
• Protein relaxiert unter Verlust von Energie über viele Zwischenschritte zurück in den Dunkelzustand.

Transportschritte

1. Lichtabsorption + Isomerisierung
2. H\(^+\) Abgabe an den ersten Akzeptor \( A_1 \)
3. Abgabe eines H\(^+ \) von \( A_2 \) ans Außenmedium
4. Reprotonierung des Retinals vom Donor 1
5. Reprotonierung des Donors \( D_1 \) aus dem Proteininneren
6. Protonenübertragung von \( A_1 \) auf \( A_2 \)

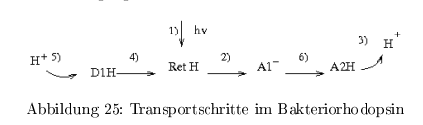
Es handelt sich um einen nicht-linearen Protonentransfer im Protein. Beobachtungen aus der 3D-Struktur zeigten, dass die Abstände zwischen Donor und Akzeptor zu groß sind --> H2O fungiert als H\(^+\)-Transfer-Mediator, wird von Konformations- und pK-Änderungen des Proteins begleitet. Die Energiebilanz beim Aufbau des elektrochem. Gradienten beträgt \( < 17\,\% \)

Photosynthese - angewandte Photochemie

Die Proteine des Photosystem I sind nicht für den Ladungstransport verantwortlich, sondern dienen der Platzierung der Co-Faktoren. Die Aufgabe der Photosynthese ist die Umwandlung von Licht in einen elektrochem. Gradienten.
Zeitliche Einordnung:

• Lichtabsorption: \( S_0\rightarrow S_1\), \( S_0\rightarrow S_2 \) in \( 10^{-15}\) sek
• Energieverlust: IC( \( S_2\rightarrow S_1 \) ), vibrational cooling in \( 10^{-12}\) sek
• Lebenszeit des \( S_1\)-Zustandes \( 10^{-8}\) sek
  • --> IC( \( S_1\rightarrow S_0 \) ) und ISC alle sehr langsam
  • --> viel Zeit für Photochemie: \( 10^{-15} \) bis \( 10^{-8} \) sek

\( \rightarrow S_1 \): Elektronenübertragung auf einen Akzeptor \( A_1 \) \[ S\,A \rightarrow S^*\,A \rightarrow S^+\,A^- \] Die Quantenausbeute beträgt: \( \phi > 0,99\). Um eine Ausbeute von 99% zu erreichen, muss \( \tau_{ubertragung} \) 100 Mal schneller sein, als die Fluoreszenz \( \tau_{Fluor}=10^{-8} \) sek. Chlorophyll ist Sensitizer (Lichteinfang) und gleichzeitig prim. e\(^-\)-Lieferant im Reaktionszentrum.

Ladungstrennung

Chlorophyll ist im angeregten Zustand ( \( S_1 \) ) stärker reduzierend als im \( S_0 \)-Zustand und der erste e\(^-\)-Akzeptor befindet sich im van-der-Waals Abstand, was dazu führt, dass das Chlorophyll ein e\(^- \) überträgt. Dabei muss die Rückreaktion verhindert werden: Stabilisierung durch Ladungstrennung. Zur Vergrößerung des Ladungsabstandes wird e\(^- \) auf 2. Akzeptor übertragen: \[ S^+-A_1^--A_2 \rightarrow S^+-A_1-A_2^- \] Dies ist Möglich, da \( A_2 \) ein positiveres Redoxpotential besitzt --> bedeutet Abfall von \( \Delta G\). Dies führt aber zu einem Verlust an thermodyn. Effizienz. Trotzdem wird die Ladungstrennung durch einen zusätzlichen Donor erhöht unter Verlust von freier Energie. \[ D-S^+-A_1-A_2^- \rightarrow D^+-S-A_1-A_2^- \]

bakt. RZ als vereinfachtes Modell

Das Reaktionszentrum des Purpurbakteriums war das erste Membranprotein, was kristallisiert werden konnte. In Abb.26 ist in blau der Protonenzyklus und in rot der e\(^-\)-Zyklus dargestellt.

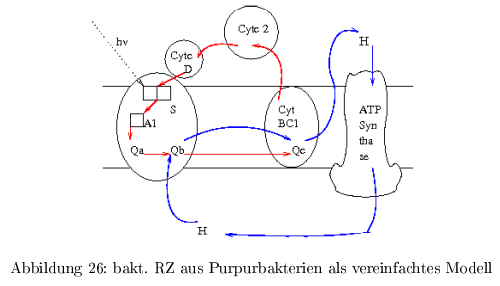
Energiespeicherung: der elektrochem. Protonengradient ( \( \Delta\mu H \) ) repräsentiert die aus dem Licht stammende

• Energie: \[ \Delta\mu H = RT\,\ln{\left(\frac{H^+_{innen}}{H^+_{ausen}}\right)} + F\Delta\phi \]
• Spannung (Protonen-potential, Protomotor. Kraft): \[ \begin{align} \Delta P &= \frac{1}{F} * \Delta\mu H*\ln{(\dots)}+\Delta\phi \\ &= \frac{1}{F}* 2,3 RT * \Delta pH + \Delta\phi \end{align} \]

Interne Prozesse im bakt. RZ

Das e\(^- \) wird vom primären Sensor S (P865, special-pair) übertragen auf \( A_1 \) (bakt. Phaeo, Phaeophytin) und danach weiter auf \( A_2 \) ( \(Q_A \), Ubiquinon), dann auf \( A_3 \) ( \(Q_B \), Ubiquinon). Als e\(^-\)-Donor dient \( Cyt_C^{2+}(D_1) \) und \( Cyt_C^{2+}(D_2)\). \[ (D_2)-D_1-P865-Phaeo-Q_A-Q_B \]

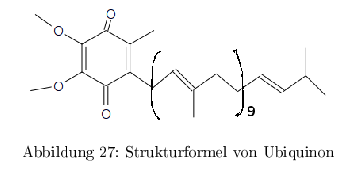
Das oxidierte \( Cyt_C^{3+} \) wandert zum bc1-Komplex und wird dort wieder reduziert.

Kombination von e\(^- \) und H\(^+ \) -Zyklus

Mit Hilfe der Absorption von 2 Photonen entstehen 2 negative Ladungen, die auf das \( Q_B \) übertragen werden und die Aufnahme von 2 Protonen ermöglicht: \[ Cyt_C^{3+} - P865 - Phaeo - Q_A - Q_BH_2 \] Dabei besitzt \( Q_BH_2 \) eine niedrigere Bindungsaffinität zur \( Q_B\)-Bindungsstelle, als \( Q_B\), \( Q_B^- \) und \( Q_B^-H \) --> \( Q_BH_2 \) verlässt das RZ und diffundiert zum \( bc1\)-Komplex. Die \( Q_B\)-Bindungsstelle wird mit oxidiertem \( Q_B \) neu besetzt (=e\(^- \) und H\(^+\)-Transporter)

Co-Faktoren Anordnung

Das bakt. RZ besteht aus 2 Untereinheiten (L,M), welche ein Heterodimer bilden. Die e\(^-\)-Überträger befinden sich in hydrophober Umgebung, was die Reduktion in Nebenreaktionen und damit die Zerstörung des Chromophors verhindert. 2 bakt. Chlorophyll A dienen als special-pair (S). Obwohl das RZ hochsymetrisch aufgebaut ist, erfolgt die e\(^-\)-Übertragung nur auf einem Weg. Auch die Abstände zwischen \( S\)-Phaeo (10A) und Phaeo-\(Q_A \) (10A) und \( Q_A\) - \(Q_B \) (15A) sind sehr ähnlich, trotzdem erfolgt die e\(^-\)-Übertragung mit sehr unterschiedlichen Geschwindigkeiten.

Markus-Theorie / Fermis Goldene Regel

Elektronenübergänge finden statt, wenn sich e\(^-\)-Potentialflächen überschneiden. Die Eigenschaften der Potentialflächen bestimmen dabei die Geschwindigkeit. Als vereinfachtes Modell dient die Darstellung als Oszillatormodell. Die Betrachtung eines Proteinkomplexes mit Donor und Akzeptor quantenmechanisch: \[ K_{et}\approx \frac{2\pi}{\hbar}\,\times |H_{AB}\ |^2 \times FC \] ( \(H_{AB}= \) elektr. Kopplungselement) und ( \(FC= \) Franck-Condon Faktor / Kernkopplung)
D.h. die e\(^-\)-Übertragungsgeschwindigkeit ist proportional zum Quadrat der elektr. Kopplung von Donor und Akzeptor und linear zur Kernkopplung und nicht von \( \Delta G \) primär abhängig.

Markus-Theorie / Franck-Condon Term

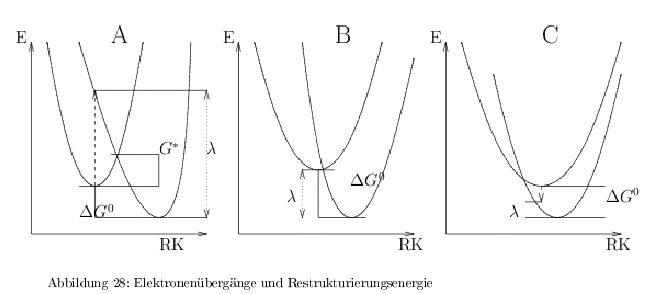
In der Abb.28 sind die 3 möglichen Potentialkurven für eine Reaktion \( D-A \rightarrow D^+A^- \) dargestellt. Die Schlüsselvariable ist dabei die Restrukturierungsenergie ( \(\lambda\) ). \[ \Delta G^* \sim \frac{-(\Delta G^0 + \lambda)^2}{4\lambda} \] -> wenn \( -\Delta G^0 = \lambda\), dann ist die Aktivierungsenergie minimal.
Geschwindigkeit: \[ K_{et} \sim \exp{\left(-\frac{\Delta G^*}{KT}\right)} = \exp{\left(-\frac{-(\Delta G^0 + \lambda)2}{4\lambda *KT}\right)} \] die Geschwindigkeit wird maximal, wenn \( \Delta G^0 = \lambda \) wie in Abb.28B und die Potentialkurve des Produktes durch das Minimum des Eduktes geht. Quantenmechanisch: Elektronenübergänge sind besonders schnell, wenn das Min. des Eduktes im Franck-Condon-Bereich des Produktes liegt. Dies ist der Fall bei \( S \) (special pair) und Phaeophytin \( A_1 \) Streng genommen gilt dieser Fall nur für den ternären Komplex \( S /Chl_A/Phaeo \). Das akzessorische \( Chl_A \) wird durchtunnelt, weil die Übertragung des e\(^- \) auf Phaeo viel schneller ist, als die Übertragung \( S \rightarrow Chl_A\), jedoch ist \(Chl_A \) für die optimale Übertragung erforderlich.

Photosystem II

• kommt in Cyanobakterien, Algen und höheren Pflanzen vor und ist eine Weiterentwicklung aus dem Reaktionszentrum der Purpurbakterien zur Wasserspaltung.
• Akzeptoren \( A_1 \) sind identisch mit dem bakt. RZ Plastoquinon befindet sich an der \( Q_B\)-Bindungsstelle, wird zu \( PQH_2 \) reduziert
• \(PQH_2 \) wandert zum \( BF6\)-Komplex (analog \( BC1\) ) die Donorseite ist identisch der im bakt. RZ

Unterschiede zum bakt. RZ

• S(680) hat ein Redoxpotential von \( + 1\,V\)
• oxidiert mit 4 Protonen 2 H2O zu O2
• auf der Akzeptorseite stabilisiert ein Mn\(_4\)-Cluster die Zwischenstufen. Die Redoxzwischenstufen des Mn-Clusters besitzen unterschiedliche Redoxpotentiale und reagieren unterschiedlich schnell

Das PS I ist nicht positiv genug um H2O zu spalten. Das PS\(^* \) II im angeregten Zusatnd ist jedoch nicht negativ genug um NADP\(^+ \) zu reduzieren. PS I ist für Reduktion von NADP\(^+ \) notwendig, um Reduktionsequivalente für den Stoffwechsel zu gewinnen. Das PS I stammt aus grünen Schwefelbakterien.

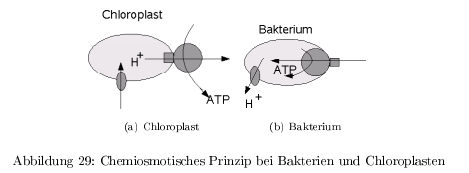
Chemiosmotische Kopplung: ATP-Synthase

ATP als Energiespeicher durch Knüpfung energiereicher Anhydridbindungen. Nutzbare Energie: \[ \Delta G _{ATP\rightarrow ADP} \approx -30\,\frac{kJ}{mol} \] Die durch Atmung und Photosynthese erzeugte Protomotorische Kraft treibt die ATP-Synthase an. Das Protomotorische Potential beträgt \( \leq 200\,mV \) = Chemiosmotisches Prinzip Bei Bakterien wird 100% der Energie zum Aufbau des protomotorischen Potentials verwendet. Bei Pflanzen nur etwa 25% und der Rest wird in Redoxpotentialen (NADPH) gespeichert.

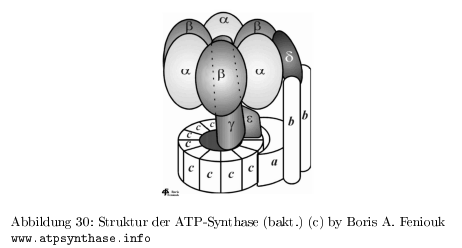
Struktur der ATP-Synthase

• besteht aus 20 Untereinheiten
• Membranteil ( \( F_0 \) ) für den Protonenfluss
• Kopfteil ( \(F_1 \) ) für die ATP-Synthase
• im Chloroplasten 12 \( C\)-Untereinheiten, im Mitochondrium 10 \( C\)-Untereinheiten
• die \( (\alpha , \beta)_3 \) Untereinheiten binden je ein Nukleotid, wobei nur die \( \beta\)-Untereinheit an der Synthese von ATP direkt beteiligt ist
• \(\gamma\)-Untereinheit wird durch den Protonenfluss gedreht
• Theorie von Boyer 1976: Konformationsänderung der \( \beta\)-Einheit führt zur ATP-Synthese, Modell einer molekularen "`Quetsche"', die Drehung der \( \gamma\)-Einheit als Ursache für die Konformationsänderung

statistische/dynamische Betrachtungen

Bei einem pH-Wert von 7 gibt es im Volumen eines Thylakoid (Membransystem der Chloroplasten) nur 0,1 freie H\(^+ \) --> es kommen etwa 10\(^4 \) protein- und lipidgebundene Protonen hinzu, welche dynamisch freigesetzt werden können. ( \( \approx 100 \mu s \) )

Erzeugen eines Drehmomentes

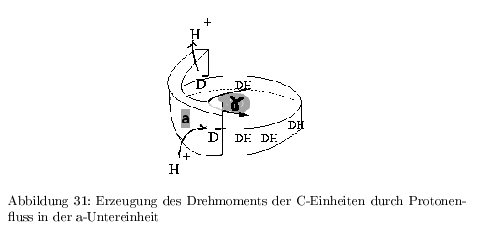
Die a-Untereinheit der ATP-Synthase definiert die Ein- und Austrittsstelle für die Protonen.

• Jede C-Untereinheit besitzt an Position 61 einen ASP-Rest, welche nur protoniert (DH) in die Lipidphase eintreten kann.
• Wahrscheinlichkeit der Protonierung von beiden Seiten hängt von der jeweiligen H\(^+\)-Konzentration ab --> erst ein Protonengradient führt zu einer einheitlichen Drehung mit bevorzugter Drehrichtung (Entropische Maschine)
• die \( \gamma \)-Untereinheit koppelt die Drehbewegung aus der H\(^+\)-Diffusion an die Konformationsänderung der \( (\alpha\beta)_3 \) Einheiten

Proton Well Hypothese

Ergänzt das Modell der \(F_0 F_1 \)ATP-Synthase um das Membranpotential. Die über die Membran abfallende Spannung erhöht den Konzentrationsunterschied an H\(^+ \) auf beiden Seiten. Elektrostatische Wechselwirkungen führt zu eine Konz.erhöhung auf der negativ geladenen Membranseite. Modell erklärt die Abhängigkeit von: \( \Delta pH \), \( \Delta U \), Anzahl der C-Untereinheiten
Chloroplast: 3 ATP/ 12 H\(^+\)
Mitochondrium: 3 ATP/ 10 H\(^+\)

Lineare Molekulare Maschinen

für Bewegung/Transport von Stoffen in der Zelle:

• Myosin: Bewegung entlang von Actin (konzertiert)
• Kinesin: entlang Mikrotubuli
• Dynein: Mikrotubuli

konvertieren Energie (ATP) in Bewegung.

Muskelkontraktion und ATP-Zyklus

Sliding Filament Modell: dicke Filamente (Myosin) und dünne (Actin) gleiten an einander vorbei \( \rightarrow \) Verkürzung \( \approx 30\% \)
klassische Beobachtung:

1. Myosin ATP-Hydrolyse \( 0,05\,\frac{1}{s} \)
2. Actin stimuliert ATP-Hydrolyse 200 fach
3. Abspaltung von ADP+P\(_i \) langsam
4. Mysosin-ADP-P\(_i\)-Komplex kann nicht durch Zugabe von ADP gebildet werden, da der Komplex der energiereichste Zustand ist!

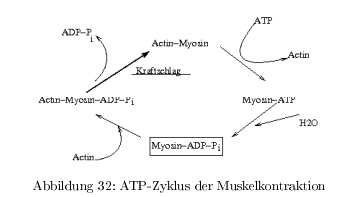
P\(_i\)-Freisetzung führt zur Bewegung des Myosinkopfes um 60° relativ zum Myosin-Arm. Bei niedriger ATP-Konz. wird der Prozess langsamer, die Schrittlänge bleibt gleich \( \Rightarrow \) ATP-Bindung und nicht Hydrolyse ist geschwindigkeitsbestimmend

Schrittlänge von Myosin

man verwendet zur Bestimmung der Schrittlänge das prozessive Myosin V, verbleibt beim Laufen auf der "Bahn":

• 1 MyoV wird an Polystyrol gebunden und dieses im Fokus eines Mikroskops gehalten (=optical Tweezer/optische Pinzette)
• MyoV wandert nach ATP-Zugabe auf dem Actin in eine Richtung (=anteriograd)
• Nachjustierung des Mikroskop-Fokus

Myosin bewegt sich mit 36nm - Schritten und überträgt dabei eine Kraft von \( 1-10\,pN \)

Laufmechanismus

1. Hand-over-Hand: ein Fuß steht fest, der andere wandert doppelte Schrittlänge
2. Inchworm-Mechanismus: beide Füße laufen die selbe Schrittlänge
3. Diffusionsmechanismus: keine klaren Schritte

Markieren von einem Bein mit ultrahellem Fluoreszenzmarker und verwenden einer Methode mit \( 1-10\,nm \) Auflösung:

1. FIONA: Nahfeld-Rastertechnik
2. TIRFM: Lasertechnik zur Oberflächenverstärkung mit hoher räumlicher Auflösung auf dünnen semitransparenten Goldfolien

Ergebnis: Myosin bewegt sich Hand-over-Hand

Unidirektionalität

Myosin bewegt sich auf dem Actin in nur eine Richtung:

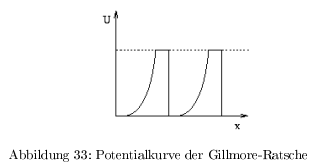
• G-Ratsche nach Gillmore: thermische Bewegung, unsymmetrisches Energieprofil führt zur Direktionalität; energetisch in beide Richtungen gleich \( \rightarrow \) geht hin und her
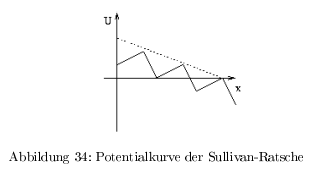
• S-Ratsche nach Sullivan: Direktionalität wird durch Energiefreisetzung bei einem definierten Schritt erreicht. Potentialgefälle;
• alle linearen Motoren setzen Energie aus ATP/GTP frei

Das ATP dient nicht der Bewegung (erfolgt durch die Brownsche Molekularbewegung) sondern zum Erzeugen der Direktionalität durch ein Potentialgefälle!

lineare Motoren II

die wichtigsten Enzyme aller zellulären Organismen ist die DNA-Polymerase (DNAP) und die RNA-Polymerase (RNAP) Die RNAP synthetisiert dabei RNA in \( 5'\rightarrow 3' \) Richtung und bewegt sich entlang des DNA-Strangs in \( 3'\rightarrow 5' \) Richtung. Dabei verrichtet die Maschine mechanische Arbeit gegen dissipative Kräfte (Bsp. Zentrifugalkräfte, hydrodynamische Kräfte, DNA/Protein Kontakte)

• RNAP bewegt sich ungerichtet auf DNA in beide Richtungen
• Polarität der Bewegung wird vermittelt durch Bindung der Bewegung an den Promotor Bindeproteine

Kraft: RNAP/DNAP bis zu 35pN und damit viel größer als Myosin/Kinesin. Kraft wird für die Polymerisation verwendet und nicht für den Transport. Die Effizienz beträgt 20% der Energie aus allen 4 Nukleotiden.

Mechanismus

Die RNAP bewegt sich progressiv auf dem (-)DNA-Strang. Am Promotor binden RNAP und Initiationsfaktoren; bildet Initiationskomplex (TIC), noch keine Synthese möglich Beim Übergang zum Elongationskomplex (TEC) verliert die RNAP ihre Sequenzspezifität und es kommt zur festen RNAP-DNA-Bindung. Nur so ist eine Synthese und Wandern auf der DNA möglich.
Reaktionszyklus:

1. Nukleotidbindung
2. Ausbildung der chem. Bindung durch Verdrängung des Pyrophosphat (pp) durch \( 3' \)-RNA-OH

Bei niedriger pppN-Konzentration oszilliert die RNAP hin und her zw. den Positionen I und I+1 oder darüber hinaus
hypertranslocation oder backtracking
Problem: läuft RNAP um die DNA oder wird die DNA vorher entwunden? \( \rightarrow \) Visualisierung der Rotation ergab: Frehmomen von \( 5\,pN \) ist erforderlich

Energetik

• RNAP oszilliert auf der DNA entsprechend dem Brownien Ratchet Modell (G-Ratsche)
• die Bindung von pppN setzt \( \approx 8\,kcal/mol \) frei
• d.h. die Bindung von Nukleotiden erzeugt durch elektrostatische WW die Kraft und führt zu einer Konformationsänderung der RNAP

\(3'\)-OH Ende der RNA führt zur Dipolverschiebung des Phosphats und damit zur Freisetzung von pp =elektrostatischer Prozess