- näherungsweise für Luft und Wasser
- für NICHT ideale Flüssigkeiten mit innerer Reibung -> Molekühle interagieren miteinander (=Newtonsche Flüssigkeiten)
1 laminarer vs. turbulenter Fluss
- der Fluss ist laminar in viskosen Medien
- turbulent in nicht-viskosen Medien
1.1 Viskosität
Die Viskosität ist ein Maß der Zähigkeit. Man bezeichnet eine Strömung als laminar, wenn die Vektoren der Strömungsgeschwindigkeit parallel zu einander ausgerichtet sind. Dabei ist charakteristisch, dass die Flüssigkeitsschichten gleichgerichtet aufeinandergleiten, gegebenenfalls parallel zu einer Grenzschicht.
Zur Charakterisierung von laminaren Strömungsprofilen ist der Begriff des Geschwindigkeitsgradienten \( (\gamma) \) wichtig. Dieser ist durch die Ableitung der Geschwindigkeit \( (v) \) entlang einer Koordinate \( (z) \) senkrecht zur Strömungsrichtung beschrieben:
\[ \gamma = \frac{dv}{dz} [s^{-1}] \]
Bewegen sich 2 planparallele Flächen gegeneinander, so ist der Geschwindigkeitsgradient \( (\gamma) \) für eine homogene Flüssigkeit zwischen den Flächen überall konstant: \( \gamma = \frac{\Delta v}{\Delta x} \) (x = Abstand der Flächen)

</div>
Für die Strömungstreibende Kraft \( (F) \) ergibt sich folgender linearer Zusammenhang:
\[ F = \eta A \gamma \]
( \( \eta = \) Reibungskoeffizient = dynamische Viskosität \( [\frac{kg}{ms}] \) oder \( [\frac{Ns}{m^2}] \) )
Es tritt also ein Reibungskoeffizient auf, der als Viskosität \( (\eta) \) bezeichnet wird. Die Viskosität gibt an, welche Kraft erforderlich ist, um bei einer Flüssigkeitsschicht der Größe \( 1\,m*1\,m*1\,m \) , die obere Schicht parallel zur Unteren mit einer Geschwindigkeit \( v=1\,m*s^{-1} \) in Bewegung zu halten. \( \eta [N\,s\,m^{-2}] = [Pa\,s] \)
Des weiteren unterscheidet man mit der kinematische Viskosität
\[ \nu = \frac{\eta}{\rho} \left[\frac{m^2}{s}\right] \]
( \( \rho = \) Dichte des Mediums) einen Parameter, der die Dichte des Mediums berücksichtigt.
Die Viskosität ist stark temperaturabhängig. Des weiteren steigt die Viskosität mit steigender Konzentration an gelöster oder suspendierter Stoffe. Bei newtonschen Flüssigkeiten ist die Viskosität unabhängig vom Geschwindigkeitsgradienten.
Scherkraft
\[ f_s=\frac{\eta * v* A}{d} \] ( \( d = \) Abstand)
viscous critical force
\[ f_{krit} = \frac{\eta*\eta}{\rho} \left[\frac{kg*m^2}{s^2}\right] \] \( \Rightarrow \) Flüssigkeit ist viskos, wenn \( \frac{f_s}{f_{krit}} \) klein ist

Fluss entlang eines Körpers
Wird eine dünne Platte \emph{parallel} zu ihrer Fläche angeströmt, so entsteht ein Strömungsprofil, dessen Charakter sich mit zunehmendem Abstand \( (l) \) von der Kante \( (l=0) \) ändert.
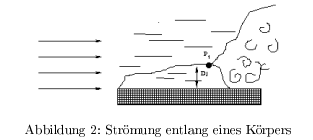
Unmittelbar an der Oberfläche befindet sich eine Haftschicht, d.h. ein dünner unbeweglicher Flüssigkeitsfilm. Mit steigendem Abstand zur angeströmten Fläche steigt die Geschwindigkeit, der Übergang zur ungestörten Strömung ist fließend. Die laminare Schicht wird mit \( \delta _L \) bezeichnet.
An einem kritischen Punkt ( \( P_t = \) Point of transition) entstehen spontane Turbulenzen. Die in der Turbulenten Strömung auftretende Reibung vergrößert die Schicht \( (\delta _T) \) bis zur ungestörten Strömung. Dieser Punkt \( (P_t) \) kann nur mit einer Wahrscheinlichkeit vorausgesagt werden.
Reynoldszahl
Die Reynoldszahl \( (R\!e) \) beschreibt das Verhältnis der inverten Kräfte zur viskosen Kraft \[ R\!e = \frac{l v \rho}{\eta} \eta=\nu \rho \Rightarrow \underline{R\!e=\frac{l v}{\nu}} \] ( \( v = \) Geschwindigkeit) und ( \( \nu = \) kinematische Viskosität)
Bremsweg
\[ \begin{align} F &= m\left(-\frac{dv}{dt}\right) = 6 \pi \eta r v \\ -\frac{dv}{dt} &= \frac{6 \pi \eta r v}{m} \\ & \\ \Rightarrow v(t) &= v(0) * \exp(-\frac{t}{\tau}) \\ & \tau = \frac{2r^2\rho}{9\eta} \end{align} \]
Hydrodynamik des Blutflusses
laminare Flüsse
Der laminare Blutfluss in Kapillaren kann als Bewegung konzentrischer Zylinder aufgefasst werden:
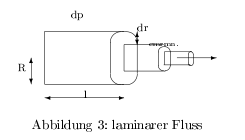
Die Schubkraft ist das Produkt aus Fläche und Druckdifferenz: \[ F_S = \pi r^2 * \Delta p \] jeder Zylinder mit der Dicke \( dr \) erfährt eine Reibungskraft proportional zum Geschw.gradienten \( \frac{dv}{dr} \) , der Zylinderfläche \( 2\pi r l \) und der Viskosität \( \eta \) : \[ F_R = 2\pi r l * \eta * \frac{dv}{dr} \] Die Reibungskraft ist dabei nicht an allen Stellen gleich. Für den stationären Zustand, wo \( F_S =F_R \) ist gilt: \[ \begin{align} \pi r^2*\Delta p &= 2\pi r l * \eta *\frac{dv}{dr} \\ &= \underbrace{\frac{\Delta p}{2l\eta}}_{\mathbf{c}} \ \intop_0^R r \ dr \end{align} \] Daraus lässt sich das Strömungsprofil durch Integration bestimmen: \[ \begin{align} v(r)&=\frac{1}{2}c R^2 - \frac{1}{2}c r^2 \\ &= \frac{dp}{dl}*\frac{1}{4\eta}\left(R^2-r^2\right) \end{align} \]
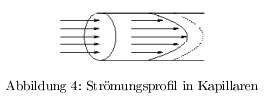
Aus dem parabelförmigen Strömungsprofil lässt sich erkennen, dass die Geschwindigkeit in der Mitte des Gefäßes am höchsten ist und das bei gleichem Druck die zentrale Strömungsgeschwindigkeit in einem großen Gefäß höher ist als in einem kleinen Gefäß.
Volumenfluss
Um den Volumenfluss zu berechnen, muss man die Funktion \( v(r) \) über das gesamte Profil des Gefäßes integrieren und erhält das
Hagen-Poiseuillesche-Gesetz
\[ J_V = \frac{\pi \Delta p R^4}{8l\eta} \] Weil der Volumenfluss \( J_V \propto R^4 \) vom Radius in der 4.\,Potenz abhängt, führen bereits kleinste Änderungen des Gefäßdurchmessers zu starken Veränderungen des Blutstroms. Das Blut ist jedoch eine NICHT-Newtonsche Flüssigkeit mit folgenden Eigenschaften
- die Viskosität \( \eta \) nimmt mit der Schergeschwindigkeit ab, d.h. das Blut wird flüssiger mit steigender Geschwindigkeit
- die Zellen aggregieren, was zu einer "Geldrollenbildung" führt
- Blut ist keine homogene Flüssigkeit und die Viskosität \( \eta \) ist so vom "`Hämatokrit"' abhängig
- starke Deformation der Zellen in engen Kapillaren
- Farhaeus-Lindquist-Effekt die Zellen konzentrieren sich in der Mitte des Gefäßes
- der Blutfluss ist pulsierend. Die Pulswellen werden durch die Elastizität der Gefäßwandungen zum Teil abgefangen und setzen sich als Druck- und Geschwindigkeitsschwankung fort. Die Geschwindigkeit der Pulswellen lässt sich durch die Moens-Korteweg-Gleichung bestimmen: \[ v_{Puls} = \sqrt{\frac{Y \ d}{2r\rho}} \] ( \( Y = \) Elastizitätsmodul = \( \frac{\sigma}{\epsilon} \) siehe Abb.6)