Zur Beschreibung des Zeitverhaltens von biochem. Reaktionen.
Reaktionstypen
Es können verschiedenen Reaktionen eine Reaktionsordnung zugeordnet werden. Formal handelt es sich um die Summe der Konzentrationsexponenten.

Wie in Tab.3 zu erkennen ist, ist die Dimension der Reaktionsgeschwindigkeit von der Reaktionsordung abhängig! Die vorhergesagten Zeitgesetze müssen experimentell überprüft werden.
Enzymkinetik
Wirkung von Enzymen
Das Enzym bildet einen Übergangskomplex mit den Ausgangsstoffen.
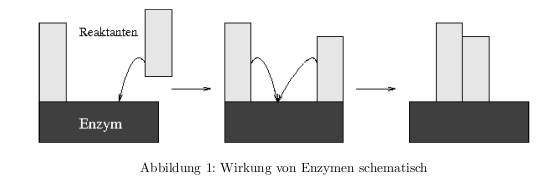
Für eine chemische Reaktion müssen Reaktionspartner in der richtigen Orientierung aufeinander treffen und aktiviert werden. Die Häufigkeit für thermische Stöße: Die Energie im Mittel \( E=kT \) und die Frequenz im Oszillatormodell \( E=\hbar\nu \) und durch gleichsetzen erhält man: \[ \nu = \frac{kT}{\hbar} = 6*10^{12}\,\frac{1}{sek} \] Mit Hilfe der Boltzmannverteilung erhält man die Häufigkeit der Stöße, die die benötigte Aktivierungsenergie \( \Delta G_R \) aufweisen: \[ h = \frac{kT}{\hbar} * \exp{\left(-\frac{\Delta G_R}{RT}\right)} \] Bei der Bildung des Enzym-Übergangskomplexes gilt: \( dG = dH -TdS \)
- Bildung des Komplexes ist entropisch ungünstig, Verlust von Freiheitsgraden
- chemische Bindung zw. Enzym und Edukten \( \rightarrow \) \( dH<0 \) kann die Gesamtbilanz optimieren
- beim Zusammenlagern kann Wasser aus der Hydrathülle frei werden \( \rightarrow \) Entropie steigt
Für das Herabsetzen der Aktivierungsenergie gilt:
- Aktivierungsenergie wird durch Mithilfe von katalytischen Gruppen des Enzyms herab gesetzt
- lokale Konzentrationserhöhung der Edukte im Enzym durch chemische Bindung an das Enzym
Für die Reaktionsgeschwindigkeit gilt die Theorie des Übergangszustandes: \[ K_{Geschw.}=\frac{kT}{\hbar} * \exp{\left(\frac{\Delta S_R}{R}\right)} * \exp{\left(-\frac{\Delta H_R}{RT}\right)} \] Zum Vergrößern der Geschwindigkeitskonstanten gelten die selben Überlegungen wie für das Optimieren von \( dG \):
- Vergrößern der Entropie des Komplexes z.Bsp. durch hydrophobe Effekte
- \( \Delta H_R < 0 \) durch Freisetzen von Bindungsenergie, Einsparen von Aktivierungsenergie
Michaelis-Menten-Kinetik
\[ E + S \rightleftharpoons ES \rightarrow E + P \] Michaelis-Menten-Gleichung: \[ v = v_{max}\frac{[S]}{[S]+K_M} \] der \( K_M \)-Wert: wenn \( [S]=K_M \rightarrow v = \frac{1}{2} v_{max} \) In der Abb.2 ist der Zusammenhang von \( K_M \) und \( [S] \) in einer typischen Sättigungskinetik dargestellt.
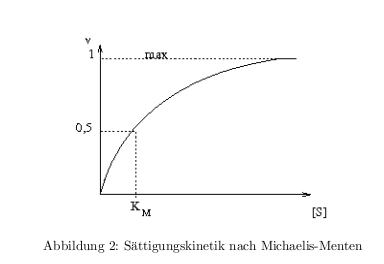
Methoden zur \( K_M \) Bestimmung
- Aus der Sättigungskurve abschätzen, jedoch sehr ungenau
- Lineweaver-Burk-Plot (Linearisierungsverfahren) \[ \frac{1}{v} = \frac{K_M}{v_{max}}*\frac{1}{[S]}+\frac{1}{v_{max}} \]
- Eadie-Hofstee-Plot (Linearisierung) \[ v = -K_M * \frac{v}{[S]}+v_{max} \]
Steuergung der Enzymaktivität
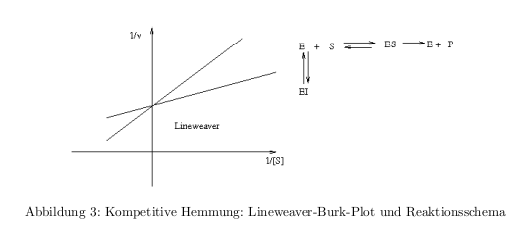
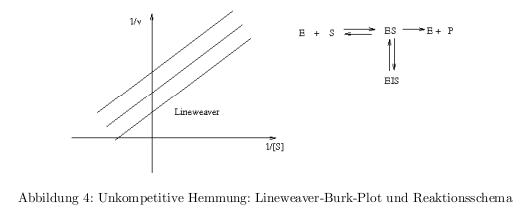
- kompetitive Hemmung: Inhibitor konkurrier mit dem Substrat um die Enzymbindung
- unkompetitive Hemmung: Inhibitor bindet an den ES-Komplex \( \rightarrow \) dead-end-Komplex trägt nicht zur Produktbildung bei
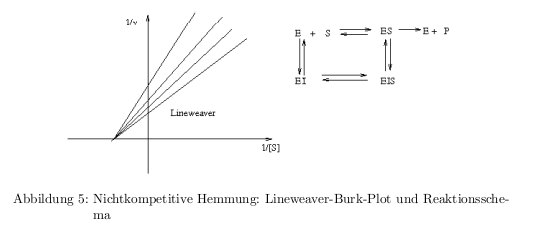
- nichtkompetitive Hemmung: Inhibitor bindet an E oder an ES und beide Komplexe tragen nicht zur Produktbildung bei
Allosterische Effekte
Der Effektor bindet an einer seperaten (allosterischen) Bindungsstelle und nicht im aktiven Zentrum \( \rightarrow \) beeinflusst Aktivität des Enzyms. Bsp: feedback-Hemmung durch Endprodukthemmung bei Syntheseketten