Mikro- und Makrozustände

Makrozustand ist eine Gruppe von Mikrozuständen mit gleichem Gesamtwert. Die Grundannahme, dass jeder Mikrozustand prinzipiell erreichbar und gleichwahrscheinlich ist, muss erfüllt sein.
Anzahl der max. Möglichkeiten: \[ \Omega_{max}=\frac{(m+n)!}{n!*m!} \] Die Gesamtanzahl der Molekühle und die Energie im abgeschlossenen System ist konstant. Schlussfolgerung: Der Makrozustand mit den meisten Mikrozuständen ist am wahrscheinlichsten!

Boltzmann-Verteilung

Voraussetzungen für die \Boltzmann-Statistik ist:

große Teilchenanzahl
System muss sich im GG-Zustand befinden
es muss sich um abzählbare "Energieportionen" \( \epsilon \) handeln

mit Hilfe der Beziehungen, dass die Teilchenanzahl im System konstant sind, die innere Energie \( U \) konstant ist und die Anzahl der Mikrozustände eines Makrozustandes maximal sein sollen, lässt sich die Boltzmann Verteilung herleiten: \[ \frac{N(\epsilon_1)}{N(\epsilon_2)}=\exp\left(-\frac{\epsilon_1-\epsilon_2}{kT}\right) \] ( \(k = \) Boltzmannkonstante (1,3806 * 10\(^{-23}\) J/K)) \[ \frac{n_1}{n_2}=\frac{c_1}{c_2} = \exp{\left(-\frac{\mu_1-\mu_2}{RT}\right)} \] Die Boltzmann-Verteilung hängt von \( T \) ab \( \rightarrow \) das GG lässt sich über die Temp. verschieben und über die Zustandssumme \( \sigma \) \[ \sigma = \sum_i\exp\left(\frac{\epsilon_i}{kT}\right) \] lassen sich alle anderen thermodynamischen Funktionen berechnen: \[ \begin{eqnarray*} U &=& \frac{N}{\sigma}*\frac{\partial\sigma}{\partial\lambda_2} \\ &\mbox{mit} & \lambda_2 = -\frac{1}{kT} \end{eqnarray*} \] des weiteren erkannte Boltzmann folgenden Zusammenhang, womit das Streben nach maximaler Entropie über die Mikrozustände eines Makrozustandes erklärbar wird. \[ S = k * \ln(\Omega) \]

Quantenmechanische Grundprinzipien

Die Wellenfunktion \( \phi \) gibt das Aufenthaltsgebiet eines Teilchens mit einer bestimmten Wahrscheinlichkeit an. \[ p_{dv}=\tilde\phi \cdot \phi \ dv \] Allgemein gilt die Berechnungsvorschrift: \[ \mbox{Eigenschaft}*\phi = \mbox{Eigenschaftsoperator}*\phi \] Aus dieser Rechnungsvorschrift folgt für ein Teilchen, was sich zwischen 2 Barrieren bewegt, die Schrödinger-Gleichung: \[ \phi_{(A)}= A * \sin(kx) + B*\cos(kx) \] mit den Randbedingungen, dass an der Barriere die Funktion Null sein muss. Weil \( \phi(0) = 0 \) und der \( \cos(0)=1 \) ist, muss \( B=0 \) sein, um die Randbedingung zu erfüllen. Dadurch vereinfacht sich die Schrödinger-Gleichung: \[ \phi(x) = A * \sin(kx) \] Für den \( \sin(kx) \) gilt die 2 Randbedingung, dass \( k*l = n*\pi\), damit der Sinus an den Barrieren eine Nullstelle hat. Wegen diesen Randbedingungen folgt, dass nur konkrete k-Werte möglich sind und damit die Energie gequantelt ist! Die Energie ist gegeben durch: \[ E = \frac{k^2 * \hbar^2}{2m} \ \mbox{mit} \ k=\frac{\pi n}{l}; n\in N \]

Methoden zur 3D-Struckturaufklärung

Röntgenbeugungsmethode

Röntgenstrahlen haben eine kleiner Wellenlänge (0,1A) als die Atomgröße (1A). Problem: keine Linsen für Röntgenstrahlen \( \rightarrow \) Mathematik muss Linse ersetzen. Phasenproblem: auf dem Röntgenfilm sind keine Phaseninformationen mehr vorhanden \( \rightarrow \) es liegen nur 50% der Informationen vor.
Ablauf:

Protein exprimieren und isolieren: 5 mg hochrein
Kristall züchten: 0,5 mm Kristalle

Problem:

hochrein, richtig gefaltetes Protein in großen Mengen
monodisperse Lösung
optimale Kristallisationsbedingungen finden: pH-Wert, Lösungszusammensetzung
Kohlenhydrate können stören
Wodurch bleiben Proteine in Lösung?
- abstoßende Kräfte: Coulomb zw. gleichen Ladungen
- ungünstige Entropiebilanz
Wodurch aggregieren Proteine?
- anziehende Kräfte: Coulomb zw. ungleichen Ladungen, Dipol-Kräfte, van-der-Waals

Thermodynamisch gilt für die Kristallbildung: \[ \Delta F = \Delta U -T\Delta S < 0 \]

\(\Delta U \) beschreibt die WW-Energie der Molekühle
Entropieänderung beim Kristallisieren ist negativ und damit ungünstig \( \rightarrow \) geringe Temperatur \( T \) begünstigt die Kristallisation
Um \( \Delta U \) zu verringern, können:
- organische Lösungsmittel verwendet werden
- Coulomb-Kräfte können über die Ladung des Proteins beeinflusst werden (pH-Wert)
- Ionenstärke des Mediums kann zum Abschirmen von Ladungen verwendet werden.
der hydrophobe Effekt von Ammoniumsulfat vermindert \( \Delta S\).

NMR-Spektroskopie

Grundprinzip: Messung von Kernspins
Dabei besitzen Atomkerne mit ungepaarten Neutronen/Protonen Spineigenschaften und verhalten sich wie atomare Magnete und können in einem externen Magnetfeld ausgerichtet werden.
starker stationärer Magnet wird zur Ausrichtung verwendet
dabei haben z.Bsp. \( ^1\)H 2 Möglichkeiten sich auszurichten: in oder entgegen der Feldrichtung
Zwischen beiden Ausrichtungen besteht ein Energieunterschied: \[ \Delta E = \gamma \hbar * B(x) \] welcher proportional zur Feldstärke des Magnetfeldes ist.
magnetisches Wechselfeld einer weiteren Spule strahlt Energie ein ( \(\Delta E = h * \nu \)) \( \rightarrow \) stört das GG, indem zusätzliche Atome in die energiereichere Ausrichtung wechseln. Über die Frequenz des Wechselfeldes können die anzuregenden Atome selektiert werden.
Energieabgabe bei der Rückkehr ins GG
die bei der Relaxation freiwerdende Energie lässt Rückschlüsse auf Nachbaratome zu
Energiebeträge sind dabei für die einzelnen H-Atome unterschiedlich, da die Feldstärke lokal durch Atomnachbarschaft verändert wird
\(\Rightarrow \) man kann zwischen den einzelnen Atomen unterscheiden

Im NMR sind alle Vorgänge sichtbar, die die Energieableitung beeinflussen.

primäre Informationen: innermolekulare Energietransfer Wege \( \rightarrow \) Bindungslängen, atomare Nachbarschaft
sekundäre Informationen: Relaxation über benachbarte Atome ermöglicht Rückschlüsse auf Struckturinformationen; kinetische Anwendungen bei chemischen Reaktionen mit ertrem hoher Zeitlicher Auflösung; dynamische Struckturinformationen
Vorteile: keine Kristalle erforderlich; Nutzung von physiologischen Lösungen; kinetische Messungen möglich
Nachteile: indirekte Technik mit hohem Einarbeitungsaufwand, schwierig bei großen Proteine; Aggregate stören

Spektroskopische Verfahren

Energie kann kinetisch und in Form von Bindungsenergie vorliegen. Gebundene Bewegungen oder zyklische Bewegungen (Drehung) sind energetisch gequantelt. Anzahl der Bewegungsfreiheitsgrade: (Man beachte den Unterschied zu den thermodyn. Freiheitsgraden) \[ FG_{mechan.}= 3 * \mbox{Atomanzahl} \] Dabei sind 3 FG für Translation, 3 FG für Rotation und die restlichen FG für Schwingungen. 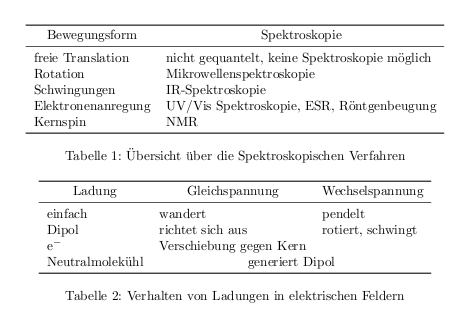Nach dem Gleichverteilungssatz speichert jeder FG die selbe Energie: \[ E= \frac{1}{2}kT \] In Tab 1 befindet sich eine Übersicht zu den spektroskopischen Verfahren. Das Messziel der Spektroskopie ist entweder der Energieverbrauch oder Details der Energieabgabe zum Zweck der Identifizierung. Die Energiezufuhr erfolgt über elektrische Felder, wobei Ladungen unterschiedliches Verhalten zeigen:
Wellenzahl: \[ \tilde\nu = \frac{1}{\lambda}=\frac{\nu}{c} \] ( \(\nu = \) Frequenz) die Wellenzahl ist proportional zur Energie
Energie eines Photons: \[ E= \hbar * \nu = \hbar * \frac{c}{\lambda} \]

UV/VIS Spektroskopie

Anregung äußerer Elektronen
Extinktion nach dem Beer-Lamberschen-Gesetz: \[ E = \frac{I_0}{I} = \varepsilon * c * d \]
man kann sowohl die Lichtabsorption als auch die Lichtemission bei der Fluoreszenzspektroskopie messen
Anwendung: FRET (Förster Resonanz-Energie-Transfer)
- angeregtes Molekül fluoresziert nicht, sondern überträgt die Energie auf ein benachbartes Molekül \[ \mbox{Fluoreszenz} \propto \frac{k_{FL}}{r^6} \]
- die Fluoreszenz ist somit proportional zum Abstand der benachbarten Moleküle, da die Energieübertragung mit steigendem Abstand unwahrscheinlicher wird
- Bsp.: Ca\(^{2+}\)-Sensor, messen der Ca\(^{2+}\)-Konzentration über Konformationsänderung des Sensors und steigender Fluoreszenz

Fourier-Spektrometer

Als Strahler wird ein schwarzer erhitzter Körper verwendet. Der Strahlengang erfolgt über mehrere parabole und planare Spiegel, so das ein Michelson-Interferometer entsteht. Ein Strahlenteiler teilt die Strahlung des schwarzen Körpers auf 2 Strahlengänge auf. Bei einem Strahlengang lässt sich mit einem beweglichen Spiegel die Gangweite variieren und so kommt es abhängig von der Frequenzdifferenz der beiden Strahlen zur Interferenz. Mit Hilfe der Fourier-Transformation kann die Interferenz in ein Spektrum umgerechnet werden.

Vorteile:

hohe (schnelle) Auflösung
Spiegeloptik \( \rightarrow \) keine Linsenfehler, bessere Lichtausnutzung
alle Wellenlängen werden verwendet (schwarzer Strahler)
Verwendung eines HeNe-Lasers als Referenz ermöglicht hohe Genauigkeit der Frequenz- oder Wellenlängen Auftragung

IR-Spektroskopie

Messung gibt Aufschluss über:

Art der Bindung
Anordnung der Atome
WW mit Nachbaratomen \( \rightarrow \) Strukturinformationen
Änderung von Bindungen (Bsp. durch Protonierung von AS)

Grundfrequenz der Schwingung: \[ f_0 = \sqrt{\frac{k}{m}} \] ( \(k= \) Kraftkonstante der Bindung) und (\(m= \) reduzierte Masse: \( m = \frac{m_1m_2}{m_1+m_2}\)) Für die Energie der Schwingung gilt: \[ E_{Schw}=\frac{n+\frac{1}{2}}{2\pi} * \hbar * f_0 \] Bei der Normalschwingungsanalyse gilt: \( E_{schw}=2\pi \ (n+\frac{1}{2}) \ \hbar f_0 \) Problem: Wasser; \( \rightarrow \) messen in \( D_2O \) oder dünnsten Schichten

Ramanspektroskopie

zur Schwingungsanalyse
als Strahlungsquelle dient polarisiertes Laser-Licht
Prinzip: Strahlung induziert schwingende Dipole
Vorteil: komplementär zu IR \( \rightarrow \) man erhält Spektren von Molekülen ohne Dipol; Wasser wirkt nicht störend; ermöglicht Spektren von biolog. Geweben

CD-Spektroskopie

circulär polarisiertes Licht als Strahlungsquelle
chirale Moleküle drehen Licht in bevorzugte Richtung \( \rightarrow \) Möglichkeit zwischen \( \alpha\)-Helix und \( \beta\)-Faltblatt zu unterscheiden
grobe Strukturbestimmung möglich

Doppler-Verbreiterung

Die Verbreiterung der Spektrallinien entsteht durch den optischen Doppler-Effekt. Durch die thermische Bewegung der Teilchen bewegen sich immer einige Teilchen relativ zum Photon. Dabei verändert sich die Photonenfrequenz relativ zum Bezugspunkt. Die Bewegung der Teilchen folgt der Boltzmann-Verteilung und so entstehen Absorptions- und Emissionslinien als Gauß-Kurve. Hinzu kommt, dass nur unendliche Wellen monochromatisch sind und die endliche Prozessdauer zu nichtchromatisch abgestrahltem Fluoreszenzlicht führt.

Statistische Thermodynamic