Mehrphasensysteme

Phasenbegriff: ist ein homogener Bereich
thermodynamische Freiheitsgrade: Anzahl der Variablen, die ein System in Gleichgewicht vollständig beschreiben

\[ \mbox{FG} = \mbox{Komponentenanzahl}-\mbox{Phasenanzahl}+2 \]

Bsp. Wasser: \( FG=1-1+2=2 \) \( \rightarrow \) Es werden 2 Variablen benötigt, um Wasser thermodynamisch vollständig zu beschreiben: \( U=U(S,p) \) oder \( U=U(T,V)\)
Bsp. Wasser+Eis: \( FG=1-2+2=1 \) \( \rightarrow \) nur eine Variable ist frei wählbar. Im Experiment legt eine Druckänderung die Temperatur fest, bei der beide Phasen nebeneinander vorliegen können.

Anwendung: Phasenseparation an Membranen

1. Effekt: Wechselwirkungen ändern sich
2. Effekt: Entropieänderung -- Einschränkung der Bewegungsfreiräume reduziert die Entropie

\( \Rightarrow \ dU=TdS-pdV+\sum dW_n \) bei konstantem Volumen ergibt sich \( dU=TdS + \sum WW \) ( \(WW = \) Wechselwirkungen) im GG: \( 0=TdS +\sum WW \) für die Temperatur des Gleichgewichts heißt dies: \( T_{GG}=\frac{\Delta WW}{\Delta S} \) Dies ist zum Beispiel wichtig für das Verständnis von Denaturierung von Proteinen oder das Schmelzen von DNA. Ausgangspunkt zum Berechnen der Ausdrücke \( \Delta WW \) und \( \Delta S \) bietet die Boltzmann-Entropieformel

Boltzmann Entropieformel

\[ S=k * \ln(W) \] ( \(k = \) Boltzmannkonstante) und ( \(W = \) Kombinationsmöglichkeiten) Ein Beispiel für die Anzahl der Kombinationmöglichkeiten \( (W)\): das Vermischen von 9Mol und 16Mol von 2 Flüssigkeiten: \( W=\frac{(9+16)!}{9!*16!} \) Ab einer ausreichend großen Molekühlanzahl kann die Stirling-Näherung verwendet werden:

Stirling-Näherung

\[ \Delta S \approx -k \left\lbrace N_A \ln(X_A)+N_B \ln(X_B) \right\rbrace \] ( \(N = \) Teilenanzahl: \( N=n*N \) und ( \(X = \) Molenbruch: \( X = \frac{n}{\sum n_i}\) ) Wenn man sich nicht für die Entropieänderung interessiert, dann kann die Lage des Gleichgewichts mittels \( \underline{\Delta G} \) charakterisiert werden.

Bestimmungsmethoden für \( \Delta G \)

Im biologischen Zusammenhang oder im Labor kann man \( \Delta T = 0 \) annehmen. Daraus ergibt sich eine alternative Gleichung: \[ \begin{eqnarray*} G &=& H - TS \\ dG &=& dH - d(TS) \rightarrow dG=dH -TdS -SdT \\ \mbox{es gilt \( \Delta T =0\)} \\ \mathbf{\Delta G} &\mathbf{=}& \mathbf{\Delta H - T\Delta S} \end{eqnarray*} \]

indirekte Messung von \( \Delta H \) und \( \Delta S\)

Vorteile: Anspruchslos: kein Labeln, kein Fixieren, automatisiert, viele Informationen, funktioniert immer bei ausreichend Probe
Nachteile: \( mg\)-Mengen erforderlich, sehr rauschanfällig da sehr sensibel, Messbereich für GG-Konstante auf \( 10^3<k<10^{12}

Isothermales-Titrations-Kalorimeter (ITC)

Kalorimeter wird mittels Thermostat auf konstanter Temperatur gehalten.
Ligand und Rezeptor werden zur Reaktion gebracht \( \rightarrow \) als Ergebnis steigt die Temperatur und man erhält \( \Delta H \) pro Tropfen Ligand
danach sinkt die Temperatur wieder auf Thermostatwert
der Anstieg der Temperatur pro Tropfen Ligand nimmt mit jedem Tropfen ab, bis alle Rezeptoren mit Liganden gebunden sind
Ergebnisse: \( \Delta H\), \( \Delta S\); GG-Konstante; Anzahl der Bindungsstellen zwischen Ligand und Rezeptormolekühl

Differential-Scanning-Calorimetry

für Phasenübegänge und Proteinfaltung
Probe und Referenz werden kontinuierlich erwärmt \( \rightarrow \) Reaktionen in der Probe führen zu Abweichungen der Heizkurve mit der der Referenz

indirekte Messung der GG-Konstanten \( (K)\)

\[ K=\frac{[RC]}{[R][C]} = e^{\left(- \frac{\Delta G}{RT}\right)} \]

Gleichverteilungssatz

Wärme wird in Bewegung gespeichert

Gleichverteilungssatz jeder Freiheitsgrad\footnote{mechanische Freiheitsgrade = ''Bewegungsmöglichkeiten''} speichert die gleiche Wärmemenge \( \left(\frac{1}{2}kT\right)\)
Möglichkeiten: Rotation, Schwingung, Translationsrichtungen

Bei einer chemischen Reaktion \( A + B \rightarrow AB \) gehen Freiheitsgrade verloren und pro Freiheitsgrad wird \( \frac{1}{2}kT \) Energie frei. Zusätzlich zur Bindungsenergie kommt es noch zu Wärme- und Entropieänderungen.

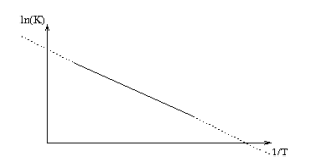
Van't-Hoff-Plot

Mit Hilfe des Van't-Hoff-Plots lässt sich nach einer Regression aus den gemessenen Werten für die Gleichgewichtskonstante (\(K\) ) und die Temperatur (\( T \) ) die gesuchten Größen \( \Delta G_0\), \( \Delta H_0 \) und \( \Delta S_0 \) berechnen. \[ \Delta G_0 = -RT \ln{K} = \Delta H_0 -T\Delta S_0 \] Die Gleichung wird nach dem Prinzip von Van't-Hoff linearisiert \[ \begin{eqnarray*} \ln{K} &=& - \frac{\Delta H_0}{R}*\frac{1}{T} + \frac{\Delta S_0}{R} \\ y &=& m x + n \\ y &=& \ln{K} \\ m &=& - \frac{\Delta H_0}{R} \\ x &=& \frac{1}{T} \\ n &=& \frac{\Delta S_0}{R} \end{eqnarray*} \]

Gleichgewichts-Dialyse:

Reaktion durch eine semipermeable Membran: Rezeptor durch die Membran eingesperrt, der Ligand kann frei diffundieren.
bekannt sind die Gesamtmenge an Rezeptor und Ligand \( [L_{ges}]\), \( [R_{ges}]\)
gesucht: \( K=\frac{[RL]}{[L]*[R]}\)
gemessen wird die \( [L] \) im GG
lösen des Gleichungssystems: \[ \begin{eqnarray*} L_{ges}&=&RL+L\\ R_{ges}&=&RL+R \mbox{(Stoffmengen)} \end{eqnarray*} \]
Vorteile: extrem einfach, preiswert
Nachteile: hohe Konzentrationen erforderlich, einer der Bindungspartner darf nicht permeable sein, die Membran kann selbst Rezeptor oder Ligand unspezifisch binden

Flugzeit-Massenspektrometrie

ein Ion wird im elektr. Feld zwischen 2 Elektroden beschleunigt
Ion verlässt Elektrodenraum und fliegt weiter zum Detektor
Messgröße: \( \Delta t \) für die Strecke bis zum Detektor

Energiezufuhr des Ions: \( E_z=q*U \) (\(q = \) Ladung des Ions) und (\(U = \) Beschleunigungsspannung) Kinetische Energie des Ions beim Austritt: \( E_k = \frac{m}{2} v^2\) \[ \begin{eqnarray*} v = \frac{d}{dt} \rightarrow &\Delta t =& \sqrt{\frac{1}{2U}}*d*\sqrt{\frac{m}{q}} \\ &=& \underbrace{\sqrt{\frac{1}{2Ue}}*d}_{Konstante} * \sqrt{\frac{m}{z}} \end{eqnarray*} \]

Massenspektrometrie von Proteinen:
- Proteine sind keine Ionen! \( \rightarrow \) fehlende Ladungen
- Lösung:Matrixmethode (MALDI)
- Einbetten in Matrixmaterial und anschließendes Verdampfen und Photooxidieren der Matrixmolekühle, bei der Oxidation entstehende Ladungen werden auf das Protein übertragen
- Elektrospray-Verfahren
- Proteinlösung wird durch geladene Kapillare gepresst, bei Verdampfen des Lösungsmittels gehen Ladungen auf Proteine über
Vorteil: sehr genau, schnell, viele Anwendungen
Nachteil: kaum für Membranproteine anwendbar, unphysiologische Einbettungsmedien

Fluoreszenz-Depolarisation

polarisiertes Licht mit einer bestimmten Schwingungsebene \( \rightarrow \) Molekühl fluoresziert nur, wenn es sich zufällig in der richtigen Lage für Absorption befindet
emittiert Fluoreszenzlicht in einer bestimmten Polarisationsebene
kleiner fluoreszierender Ligand rotiert schneller als der größere Komplex
Drehung führt zur Änderung der Polarisationsebene des Angestrahlten Lichts (Depolarisation) \( \rightarrow \) Unterscheidung der Molekülgröße möglich
bestimmen der GG-Konstanten
Vorteil: sensitiv, funktioniert auch in vivo, kleine Tropfmengen sind ausreichend
Nachteil: Labeling notwendig
Zeitskala: Absorption: \( 10^{-15}sek\); Fluoreszenz: \( 10^{-8}sek\); Molekülrotation: \( 10^{-10}-10^{-12}sek\)

Surface Plasmon-Resonanz

Glasprisma wird an der Oberseite mit einem Goldfilm bedampft \( \rightarrow \) Anker für Proteine
über Thio-Gruppen werden Rezeptorproteine verankert
Laserstrahl wird an der Goldschicht reflektiert (Reflexion ist von der Schichtdicke abhängig)
Ligand wird über die Rezeptoren eingeströmt und kann Bindung eingehen
Lichtschwächung des Lasers steigt durch höheren Brechungsindex und stehende Wellen am Goldfilm
Lichtschwächung ergibt Belegungsdichte und GG-Konzentrationen
Vorteil: Goldspots können sehr klein sein \( \rightarrow \) abscannen von großen Arrays; hohe Auflösung kleinster Konzentrationen, keine Markierung der Bindungspartner nötig, Messung der Bindungskinetik möglich
Nachteil: ein Bindungspartner muss chemisch am Goldfilm immobilisiert werden, unspezifische Bindungen auf der Goldschicht wirken störend

Absorptionsspektroskopie

messen der Extinktion abhängig von der Wellenlänge \( \lambda \) \[ E(\lambda)=\log \left(\frac{I_0}{I}\right) \]
Anwenden des Beer-Lamber-Gesetzes: \[ c = \frac{E(\lambda)}{\epsilon * d} \] mit dem Extinktonskoeffizienten ( \(\epsilon\) ) und der Küvettendicke ( \(d\) )
zur Bestimmung der Konzentration von 2 Stoffen muss bei 2 Wellenlängen gemessen werden: \[ \begin{eqnarray*} E_{\lambda_1} &=& [A]*\underbrace{\epsilon_{A\lambda_1}d}_{\mbox{bekannt}} + [B]*\underbrace{\epsilon_{B\lambda_1}d}_{\mbox{bekannt}} \\ E_{\lambda_2} &=& [A]*\underbrace{\epsilon_{A\lambda_2}d}_{\mbox{bekannt}} + [B]*\underbrace{\epsilon_{B\lambda_2}d}_{\mbox{bekannt}} \end{eqnarray*} \]