- isoliertes oder abgeschlossenes System: idealisiertes System, das weder Energie noch Materie mit der Umwelt austauschen kann
- geschlossenes System: nur Energieaustausch möglich
- offenes System: kann sowohl Energie wie als auch Materia austauschen
1. Hauptsatz
- Energie im abgeschlossenen System ist eine Erhaltungsgröße
- Energiezufuhr nur über Wärmezufuhr und Arbeit möglich
- Wärme ist eine besondere Energieform
\[ dU = \delta Q + \delta W \] ( \(dU\): Zustandsfkt;\( \delta\): keine Zustandsfkt.) Daraus folgt, dass die Energie eines Systems nur von Außen geändert werden kann. Es gibt 2 Grundlegende Energieformen: Wärme und Arbeit.
- Zustandsfkt. Wert der Funktion hängt nicht von der Vorgeschichte ab, sondern nur vom Endzustand. Wärme ist keine Zustandsfkt., da Wärme nicht unbedingt in Wärme gespeichert wird.
- intensive Parameter sind nicht additive Parameter, d.h. nicht von der Grüße des Systems abhängig z.Bsp. Wärme
- extensive Parameter sind additive Parameter z.Bsp. Masse und Volumen
Wärmeinhalt
Berechnung des Wärmeinhalts von Substanzen:
\[
dQ = m * C * dT
\]
( \(C =\) spezifische Wärmekapazität) Wasser
Wärmekapazität:\( C_{H_2O}= 4,187 [\frac{J}{g*K}] \) H-Brücken müssen beim Erwärmen gelöst werden\( (\approx -10\,\frac{kJ}{mol})\). H-Brücken sind stärker als thermische Energie bei Raumtemperatur ( \(\approx 2,5\,\frac{kJ}{mol}\) ). Zusätzliche Eigenschaften von Wasser:
- hohe Verdampfungswärme: H-Brücken müssen überwunden werden
- hohe Oberflächenspannung: durch zusätzliche Bindungskräfte
- hohe Viskosität: zusätzl. Bindungskräfte
- hoher Siedepunkt
- hoher Gefrierpunkt
- hohe Wärmekapazität
- Dichteanomalie: Eis schwimmt, 4°C höchste Dichte
- Gaslöslichkeit sinkt mit steigender Temperatur
Anwendung von Zustandsfunktionen
-
Heßscher Satz die Energiebilanz für chem. Reaktionen ist unabhängig vom Syntheseweg.
mathematische Eigenschaften
\[ \begin{eqnarray} U &=& U(p,T) \\ dU(p,T)&=&\frac{\partial U}{\partial p}dp + \frac{\partial U}{\partial T}dT \end{eqnarray} \] Es gilt der Satz von Schwarz: die gemischten Ableitungen sind gleich \[ \frac{\partial U^2}{\partial p \partial T} = \frac{\partial U^2}{\partial T \partial p} \] Ein Beispiel zur Anwendung des Schwarz'schen Satzes: \[ \begin{eqnarray*} V = V(A,B) &\Rightarrow& dV(A,B) = \frac{\partial V}{\partial A} dA + \frac{\partial V}{\partial B} dB \\ & & \frac{\partial V}{\partial A} = B \frac{\partial V}{\partial B} = A \\ &\Rightarrow& dV(A,B) = BdA + AdB \\ \Rightarrow \frac{\partial V^2}{\partial A \partial B} = \frac{B}{\partial B} = 1 & & \frac{\partial V^2}{\partial B \partial A} = 1 \\ & & \underline{1=1} \\ & & \underline{\mbox{\(V(A,B) \) ist eine Zustandsfunktion}} \end{eqnarray*} \]
- innere Energie eines Systems ist die Energiemenge, mit der man das System nachbauen könnte: \[ U(S,V,n) \Rightarrow dU = \frac{\partial U}{\partial S} dS + \frac{\partial U }{\partial V} dV + \frac{\partial U}{\partial n} dn \]
- chemisches Potential ist die Energie um ein Mol der Substanz zu erzeugen und in das System einzufügen \[ \begin{eqnarray*} \mu = \left( \frac{\partial U(T,V,n)}{\partial n} \right)_{T,V = const.} \end{eqnarray*} \]
2. Hauptsatz
- die Entropie in einem abgeschlossenen System kann nicht kleiner werden
- bleibt die Entropie gleich, befindet sich das System im Gleichgewicht
\[ dS = \frac{dQ}{T} \]
- Wärmeenergie lässt sich nur mit Gradienten nutzen
- Entropieenergie\( S*T \) beschreibt die ohne Temperaturgradienten nicht nutzbare Energie
Fundamentalgleichungen
- reversible Zustandsänderung beschreibt einen Vorgang, der restlos/spurlos umkehrbar ist \[ \begin{eqnarray*} \mbox{1.HS:}\ dU &=& \delta Q + \delta W \\ \oint dU &=& \oint \delta Q + \oint \delta W = 0 \end{eqnarray*} \] Wenn alle Änderungen\( \Delta Q \) und\( \Delta W \) im Kreisprozess verschwinden, dann gilt für reversible Änderungen:\( \underline{dU = dQ + dW} \) und mit\( dU=TdS \) gilt:\( \underline{dU=TdS + dW}\)
Beispiele für Arbeitsleistung\( dW\):
- Volumenarbeit:\( -pdV\)
- chemische Arbeit:\( \mu dn\)
- elektr. Arbeit:\( \Phi dq \) für die Energie gilt:\( \int_0^\Phi{\Phi (x) dq}\)
- Grenzflächenarbeit:\( \sigma dA\)
- Hubarbeit:\( mg*dh\)
- allgemein:\( dW = \mbox{intensive Größe/unabhängige Größe}*\mbox{extensive Größe/zur Systemgröße proportional}\)
Gibbssche Fundamentalformel
\[ dU = TdS - pdV + \sum{dW} \]
Die vielen Gesichter von\( \mathbf{dU} \)
Nach dem 1.Hauptsatz der Thermodynamik ist\( dU = dQ + dW\). Die innere Energie eines Systems gibt an, welche Energie vom Nachbauen eines Systems notwendig ist und besteht aus einem Wärmeanteil und verschiedenen Arbeitstermen. Je nach System sind verschiedene Arbeitsterme notwendig. Die Wärmeänderung\( dQ \) steht mit der Entropie über die Temperatur in Verbindung:\( dQ = TdS\). Diesen Zusammenhang kennt man von der Entropieberechnung:\( dS=dQ/T\). Um die Entropieänderung zu erhalten, wird einem System kleine Wärmemengen zugeführt und man misst die resultierende Temperatur. Daraus folgt als allgemeinste Form für\( dU\): \[ dU = TdS + dW \] Ein konkretes System kann also z.Bsp. von\( S,T,V,n \) abhängig sein. Dann ergibt sich folgende Fundamentalgleichung: \[ \begin{eqnarray*} U &=& U(S,T,V,n)\\ dU &=& \frac{\partial U}{\partial S}dS + \frac{\partial U}{\partial T}dT + \frac{\partial U}{\partial V}dV + \frac{\partial U}{\partial n}dn \end{eqnarray*} \] An Hand des Quadrates in Sec."Abhängigkeit der thermodyn. Potentiale" lässt sich die Abhängigkeit von\( dS \),\( dT \) und\( dV \) ablesen, man beachte das Vorzeichen, was aus der Pfeilrichtung hervor geht. Man beachte zusätzlich, dass\( dn \) vom chemischen Potential\( \mu \) abhängig ist. Es ergibt sich also die Fundamentalgl.: \[ dU= TdS -SdT - pdV + \mu dn \] Wie der Vergleich mit der allgemeinen Form von\( dU \) zeigt, handelt es sich um die Wärmeänderung\( dQ = TdS \) und 3 weitere Arbeitsterme\( dW\). Dieses Beispiel zeigt, dass die Fundamentalgleichung für\( dU \) vom betrachteten System abhängt und sich immer auf die allgemeine Form zurückführen lässt und der 1.Hauptsatz erfüllt ist.
Weitere thermodyn. Zustandsfunktionen
- innere Energie Energie zum Nachbauen eines Systems\( U(S,T,V,n)=TS-pV+\sum{\mu_i n_i} \) (chemische Arbeit = chem. Potential\( * \) Stoffmenge)
- Enthalpie\( H(S,p,n)=U+pV\)
- freie Enthalpie\( G(T,p,n)=U-TS+pV\)
- freie Energie\( F(T,V,n)=U-TS\)
Beispiel zum Aufstellen einer Fundamentalgleichung: \[ \begin{eqnarray*} F &=& F(T,V,n) \\ dF &=& \frac{\partial F}{\partial T} dT + \frac{\partial F}{\partial V}dV + \frac{\partial F}{\partial n}dn \\ dF &=& dU -d(TS) = dU -TdS - SdT \mbox{für dU die Gibbssche Fundamentalgleichung einsetzen}\\ dF &=& TdS - pdV + \sum{dW} - TdS - SdT \\ \mathbf{dF} &\mathbf{=}& \mathbf{-pdV + \sum{dW} -SdT} \end{eqnarray*} \]
abgeschlossenes System im GG
Ein abgeschlossenes System befindet sich im Gleichgewicht. Daraus folgt:\( dS=0 \) Das abgeschlossene System lässt sich gedanklich in Teilsysteme unterteilen, dann gilt für diese\( dS=dS_1+dS_2 = 0\).
- Fundamentalgleichung für\( dU \) nach\( dS \) umstellen: \[ \begin{eqnarray*} dU &=&TdS -pdV + \mu dn \\ dS &=&\frac{1}{T} (dU +pdV - \mu dn) \end{eqnarray*} \]
- gleichsetzten von\( dS \) beider Teilsysteme
- Ausnutzen der Erhaltungsgrößen: \[ \begin{eqnarray*} n=n_1+n_2 &\rightarrow& dn=0 \\ &\Rightarrow& dn_1 = -dn_2 \\ & & dU_1 = -dU_2 \\ & & dV_1 = -dV_2 \end{eqnarray*} \]
Daraus ergibt sich: \[ \begin{eqnarray*} (\frac{1}{T_1}-\frac{1}{T_2}) dU_1 + (\frac{p_1}{T_1}-\frac{p_2}{T_2}) dV_1 + (\frac{\mu _1}{T_1}-\frac{\mu _2}{T_2}) dn_1 = 0 \end{eqnarray*} \] Damit diese Gleichung erfüllt ist, müssen die Terme in den Klammern 0 werden. Daraus ergeben sich folgende Gleichgewichtsbedingungen:
- \(T_1 = T_2\)
- \(p_1 = p_2\)
- \( \mu _1 = \mu _2 \) Dies stellt die wichtigste alternative GG-Bedingung da. Die chemischen Potentiale aller Teilchen müssen gleich sein
weitere GG-Bedingungen sind
- \(dG = 0 \) bzw.\( dG_1=-dG_2\), wenn\( dT=0\),\( dp=0 \) und\( dn=0\)
- \(dF=0\)
- \(dH=0\)
- \(dU=0\), wenn\( dS=0\),\( dV=0\),\( dn=0\)
- \(dS=0\)
Das ideale Gasgesetz
Ein ideales Gas wird durch ausdehnungslose Punkte ohne Wechselwirkungen beschrieben. \[ \begin{eqnarray*} pV = n R T \\ p= \frac{n}{V} R T = c R T \end{eqnarray*} \] (R = Gaskonstante) und (c = Konzentration)
\(\Delta\) G für allgemeine chemische Reaktionen
Es ist eine allgemeine Reaktion gegeben:\( aA + bB \rightarrow cC + dD \) Daraus ergibt sich folgender Ansatz für\( \Delta G\): \[ \begin{eqnarray*} dn_A &=& \mathbf{-}a * d \xi\\ dn_C &=& \mathbf{+}c*d \xi \\ \Delta G &=& \sum{\mu _i dn_i} = \sum{\mu _i V_i d\xi}\\ &=& -\mu _A *a*d\xi - \mu _B *b*d\xi + \mu _C *c*d\xi + \mu _D *d*d\xi \\ \mu &=& \mu _0 + RT \ln{a} \\ a \approx c\\ \mbox{Fall\( d\xi = 1\):} & &\\ \Delta G &=& (c\mu _C +d\mu _D - a\mu _A -b\mu _B)d\xi\\ \Delta G_{(1)} &=& c(\mu _C^0 + RT\ln{c_C}) + d(\mu _D^0 +RT\ln{c_D}) - \dots\\ &=& (c\mu _C^0 +d\mu _D^0 -a\mu _A^0 -b\mu _B^0)+RT\ln{\frac{c_C^c * c_D^d}{c_A^a * c_B^b}}\\ \mathbf{\Delta G_{(1)}} &\mathbf{=}& \mathbf{(k)+RT\ln\frac{[C]^c [D]^d}{[A]^a [B]^b}} \\ \mathbf{\Delta G} &\mathbf{=}& \mathbf{\Delta G_0 + RT\ln{(K)}} \end{eqnarray*} \] ( \(\xi \) = Reaktionslaufzahl) und ( \(V_i= \) Vorzeichenbehafteter Stochiometrischer Koeffzient) und ( \(\mu \) = chem. Potential) und ( \(\mu _0 \) = chem. Potential reiner Substanz) und ( \( \ln a= \) Korrektur bei Verdünnung) und ( \(c \) = Konzentration als Näherung der Aktivität\( a \) ) An Hand der Gleichung ist erkennbar, dass\( \Delta G \) Temperatur- und Konzentrationsabhängig ist.
\( \Delta G \) für Ionen
Für Ionen gilt:\( \Delta G = \sum\tilde\mu_i \) ( \(\tilde\mu \) = elektrochemisches Potential)\( dn_i \Big|_{dT=0 \ dp=0} \) in Worten:\( \Delta G \) ist die Summe der elektrochemischen Potentiale multipliziert mit den Stoffmengen bei konstanter Temperatur und konstantem Druck. \[ \tilde\mu _i = \mu _i^0 + RT\ln(c) + z F\phi \] ( \(z= \) Ladungszahl) und ( \(F= \) Faradaykonstante) und ( \(\phi= \) elektriches Potential)
Herleitung der Nernstgleichung
Es ist ein Gefäß mit einer permeablen Membran für\( Na^+ \) gegeben. Bedingung für die Nernstgleichung: nur 1 Ionensorte kann die Phasengrenze überwinden. \[ \begin{eqnarray*} \Delta G &=& (\mu _{Na^+(1)}^{0} - \mu _{Na^+(2)}^{0})+RT\ln\frac{[Na^+]^{(1)}}{[Na^+]^{(2)}}+F(\phi _1 -\phi _2) \\ \mbox{im GG gilt\( \Delta G = 0\)} & & \\ \phi _1 -\phi _2 &=& - \frac{RT}{F}\ln\frac{[Na^+]^{(1)}}{[Na^+]^{(2)}} \\ & & \\ \mathbf{\phi _1 - \phi _2} &\mathbf{=}&\mathbf{+\frac{RT}{F}\ln\frac{[Na^+]^{(2)}}{[Na^+]^{(1)}}} \end{eqnarray*} \]
Die Goldmann-Formel
\[ \Delta \phi = \frac{RT}{F} \ln\left( \frac{p_1 c_{1,1}^+ + p_2c_{2,1}^+ + p_3c_{3,2}^- \dots}{p_1c_{1,2}^+ + p_2c_{2,2}^+ + p_3c_{3,1}^-}\right) \] ( \(p =\) Permeabilität) und ( \(c_{1,2} =\) Konzentration von Ion 1 in Phase 2) Man beachte, dass die Terme für Kationen und Anionen unterschiedlich eingehen!
Abhängigkeit der thermodyn. Potentiale
Das folgende Diagramm veranschaulicht die Abhängigkeit der thermodynamischen Potentiale:
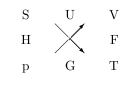
Dabei muss das Diagramm wie folgt gelesen werden: Ein thermodyn. Potential (\(U,F,G,H\) ) ist von den anliegenden Größen rechts und links abhängig. Z.Bsp.\( F=F(V,T) \) Um das totale Differential (\(dF= \pm ?dV \pm ?dT\)) zu erhalten, muss entlang der Pfeile gegangen werden. Die Richtung der Pfeile gibt dabei das Vorzeichen an. Wenn also entgegen der Pfeilrichtung gegangen wird, ist das Vorzeichen negativ. Um also die Zustandsfunktion für\( F \) zu erhalten, muss man von\( V \) entgegen dem Pfeil zu\( p \) gehen:\( dF = -pdV \pm ?dT \) und von\( T \) entgegen der Pfeilrichtung zu\( S\). \[ \Rightarrow dF= -pdV - SdT \]